题目内容
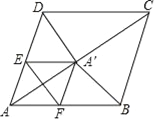
【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为_____.
【答案】![]() 或
或![]() .
.
【解析】首先证明四边形AEA′F是菱形,分两种情形:①CA′=CD,②A′C=A′D分别计算即可.
解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CD=CA′时,∵AA′=AC﹣CA′=3,
∴AP=![]() AA′=
AA′=![]() .
.
②当A′C=A′D时,∵∠A′CD=∠A′DC=∠DAC,
∴△A′CD∽△DAC,
∴![]() =
=![]() ,
,
∴A′C=![]() ,
,
∴AA=8﹣![]() =
=![]() ,
,
∴AP=![]() AA′=
AA′=![]() .
.
故答案为![]() 或
或![]() .
.
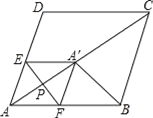
“点睛”本题考查菱形的性质、翻折变换、等腰三角形的判断和性质等知识,解题的关键是学会分类讨论,不能漏解. 属于中考常考题型.

练习册系列答案
相关题目