Question

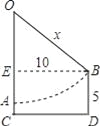
【题目】如图，面积为8的矩形ABOC的边OB、OC分别在x轴、y轴的正半轴上，点A在双曲线y＝的图象上，且AC＝2．

（1）求k值；

（2）矩形BDEF，BD在x轴的正半轴上，F在AB上，且BD＝OC，BF＝OB．双曲线交DE于M点，交EF于N点，求△MEN的面积．

Answer 1

【答案】(1)y＝；(2)

【解析】试题分析：（1）根据矩形的面积求出AB，求出A的坐标，代入反比例函数解析式求出即可；

（2）先求出BF和OD，代入函数解析式求出点的坐标，求出EN和EM，根据面积公式求出即可．

试题解析：解：（1）∵矩形ABOC的面积为8，AC=2，∴OC=AB=8÷2=4，AC=OB=2，∴A点的坐标为（2，4），∵点A在双曲线的图象上，∴代入得：k=8；

（2）由（1）知：反比例函数的解析式为，∵BD=OC，BF=OB，OC=4，OB=2，又∵四边形BDEF是矩形，∴BD=EF=4，BF=DE=2，OD=BD+OB=6，把y=2代入得：x=4，即N点的坐标为（4，2），把x=6代入得：y=，即M的坐标为（6， ），∴EN=6﹣4=2，EM=2﹣=，∴△MEN的面积为=．