��Ŀ����
����Ŀ��һ����װ��������ˮ�ܺ�һ����ˮ�ܵ�������ÿ���ӵĽ�ˮ���ͳ�ˮ����������������������ˮ�ܵĽ�ˮ�ٶ���ͬ����ˮ�ܺͳ�ˮ�ܵĽ���ˮ�ٶ���ͼ1��ʾ��ijʱ�̿�ʼ��6���ӣ����ٴ�һ��ˮ�ܣ�����������ˮ��y����λ��������ʱ��x��ͼ2��ʾ��
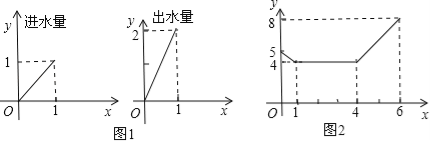
��1�����ж�0��1�֡�1�ֵ�4�֡�4�ֵ�6��������ʱ��εĽ�ˮ�ܺͳ�ˮ�ܴ������
��2����4��x��6ʱ��y��x�仯�ĺ�����ϵʽ��
��3��6���Ӻ���ͬʱ������ˮ�ܣ���10����ʱ������ˮ���Ƕ�������
���𰸡�1��0��1�֣���һ����ˮ�ܣ���һ����ˮ�ܣ�1�ֵ�4�֣�������ˮ�ܺ�һ����ˮ��ȫ����4�ֵ�6�֣���������ˮ�ܣ��رճ�ˮ�ܣ���2��y=2x-4����3��16����
��������
�⣺��1�� 0��1�֣���һ����ˮ��, ��һ����ˮ��
1�ֵ�4�֣�������ˮ�ܺ�һ����ˮ��ȫ����
4�ֵ�6�֣���������ˮ�ܣ��رճ�ˮ������������������3��
��2����4��x��6ʱ������ͼ����㣨4��4����6��8��. ������������������1��
�����ʽΪ![]() ��������ã�
��������ã�![]() ������������������2��
������������������2��
���:![]() ������������������4��
������������������4��
����������ʽΪ![]() ������������������5��
������������������5��
��3����ͬʱ��һ����ˮ�ܣ�һ����ˮ�ܣ���10����ʱ������ˮ����8+��-1����4=4��
���������������� 2��
��ͬʱ��������ˮ�ܣ���10����ʱ������ˮ����8+2��4=16������������4��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�