题目内容
【题目】如图,Rt△ABC中,∠ABC=90°,DE垂直平分AC,垂足为O,AD∥BC,且AB=5,BC=12,则AD的长为 . 
【答案】![]()
【解析】解:连接AE. 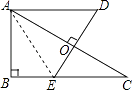
∵DE是线段AC的垂直平分线,
∴AE=EC.
设EC=x,则AE=EC=x,BE=BC﹣EC=12﹣x,
∵在直角△ABE中,AE2=AB2+BE2 ,
∴x2=52+(12﹣x)2 ,
解得:x= ![]() .
.
即EC= ![]() .
.
∵AD∥BC,
∴∠D=∠OEC,
在△AOD和△COE中, ,
,
∴△AOD≌△COE,
∴AD=EC= ![]() .
.
故答案是: ![]() .
.
【考点精析】本题主要考查了线段垂直平分线的性质和勾股定理的概念的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

【题目】某运动员在一场篮球比赛中的技术统计如表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 | 罚球得分 | 篮板 | 助攻(次) | 个人总得分 |
数据 | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中线重合,这样得到图②,图③,… 
(1)观察以上图形并完成下表:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图(n)中,菱形的个数为(用含有n(n≥3)的代数式表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .