题目内容
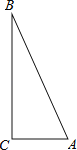
【题目】如图,![]() 中,
中,![]() , 点
, 点![]() 在线段
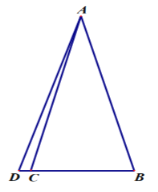
在线段![]() 的延长线上, 连接AD,CD=1,BC=12,∠DAB=30°, 则
的延长线上, 连接AD,CD=1,BC=12,∠DAB=30°, 则![]() __________.
__________.
【答案】4![]()
【解析】
过点B作BE⊥AD于点E,AH⊥BC于H.设AB=AC=x.根据AE+DE=AD,分别利用勾股定理求出AE,DE,AD,构建方程即可解决问题.
解:过点B作BE⊥AD于点E,AH⊥BC于H.设AB=AC=x.
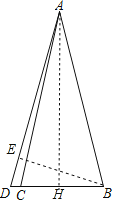
在Rt△ABE中,
∵∠BAE=30°,AB=x,
∴BE=![]() AB=
AB=![]() x,AE=
x,AE=![]() BE=
BE= ![]() x,
x,
∵AB=AC,AH⊥BC,
∴CH=BH=6,
在Rt△AHB中,AH2=x2-62,
在Rt△DBE中,DE=![]() ,
,
在Rt△ADH中,AD=![]() .
.
∵AE+DE=AD,
∴![]() ,
,
整理得:x4-13×51x-(12×13)2=0,
解得x2=13×48或13×3(舍去),
∵x>0,
∴x=4![]() ,
,
经检验:x=4![]() 是无理方程的解,
是无理方程的解,
∴AC=4![]() ,
,
故答案为4![]() .
.

练习册系列答案
相关题目