Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥°į◊ŘļŌ”Ž Ķľý°Ī–°◊ťŅ™’ĻŃň≤‚ŃŅĪĺ–£∆žłňłŖ∂»Ķń ĶľýĽÓ∂Į£¨ňŻ√«÷∆∂©Ńň≤‚ŃŅ∑Ĺįł£¨≤ĘņŻ”√Ņő”ŗ ĪľšÕÍ≥…Ńň ĶĶō≤‚ŃŅ.ňŻ√«‘ŕ∆žłňĶ◊≤Ņňý‘ŕĶń∆ĹĶō…Ō£¨—°»°ŃĹłŲ≤ĽÕ¨≤‚Ķ„£¨∑÷Īū≤‚ŃŅŃňł√∆žłň∂•∂ňĶń—ŲĹ«“‘ľį’‚ŃĹłŲ≤‚Ķ„÷ģľšĶńĺŗņŽ.ő™Ńňľű–°≤‚ŃŅőů≤Ó£¨–°◊ť‘ŕ≤‚ŃŅ—ŲĹ«Ķń∂» ż“‘ľįŃĹłŲ≤‚Ķ„÷ģľšĶńĺŗņŽ Ī£¨∂ľ∑÷Īū≤‚ŃŅŃňŃĹīő≤Ę»°ňŁ√«Ķń∆Ĺĺý÷Ķ◊ųő™≤‚ŃŅĹŠĻŻ£¨≤‚ŃŅ żĺ›»ÁŌ¬ĪŪ(≤ĽÕÍ’Ż)
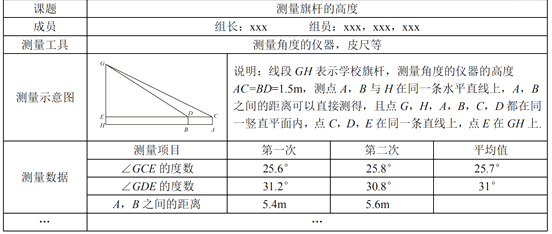

»őőŮ“Ľ£ļŃĹīő≤‚ŃŅA£¨B÷ģľšĶńĺŗņŽĶń∆Ĺĺý÷Ķ « m.
»őőŮ∂Ģ£ļłý囓‘…Ō≤‚ŃŅĹŠĻŻ£¨«Žń„įÔ÷ķ°į◊ŘļŌ”Ž Ķľý°Ī–°◊ť«ů≥Ų—ß–£—ß–£∆žłňGHĶńłŖ∂».
(≤őŅľ żĺ›£ļsin25.7°„°÷0.43£¨cos25.7°„°÷0.90£¨tan25.7°„°÷0.48£¨sin31°„°÷0.52£¨cos31°„°÷0.86£¨tan31°„°÷0.60)
»őőŮ»ż£ļł√°į◊ŘļŌ”Ž Ķľý°Ī–°◊ť‘ŕ∂®÷∆∑Ĺįł Ī£¨Ő÷¬ŘĻż°įņŻ”√őÔŐŚ‘ŕ—ŰĻ‚Ō¬Ķń”į◊”≤‚ŃŅ∆žłňĶńłŖ∂»°ĪĶń∑Ĺįł£¨ĶęőīĪĽ≤…ń….ń„»Ōő™∆š‘≠“ÚŅ…ń‹ « ≤√ī£Ņ(–ī≥Ų“ĽŐűľīŅ…).
°ĺīūįł°Ņ»őőŮ“Ľ£ļ5.5£Ľ»őőŮ∂Ģ£ļ∆žłňGHĶńłŖ∂»ő™14.7m£Ľ»őőŮ»ż£ļľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
»őőŮ“Ľ£ļņŻ”√∆Ĺĺý żĻę ĹĹÝ––ľ∆ň„ľīŅ…Ķ√£Ľ
»őőŮ∂Ģ£ļ”…Ő‚“‚Ņ…Ķ√£ļňńĪŖ–őACDB£¨ňńĪŖ–őACEH∂ľ «ĺō–ő£¨‘Ú”–EH=AC=1.5£¨CD=AB=5.5£¨…ŤEG=x m£¨‘ŕRt°ųDEG÷–£¨ņŻ”√°ŌGDEĶń’ż«–Ņ…Ķ√![]() £¨‘ŕRt°ųCEG÷–£¨ņŻ”√°ŌGCEĶń’ż«–Ņ…Ķ√CE=
£¨‘ŕRt°ųCEG÷–£¨ņŻ”√°ŌGCEĶń’ż«–Ņ…Ķ√CE=![]() £¨‘Ŕłýĺ›CD=CE-DE£¨Ņ…«ůĶ√xĶń÷Ķ£¨‘Ŕłýĺ›GH=CE+EHľīŅ…«ůĶ√īūįł£Ľ
£¨‘Ŕłýĺ›CD=CE-DE£¨Ņ…«ůĶ√xĶń÷Ķ£¨‘Ŕłýĺ›GH=CE+EHľīŅ…«ůĶ√īūįł£Ľ
»őőŮ»ż£ļ–ī≥ŲĶńņŪ”…÷Ľ“™ļŌņŪľīŅ….
»őőŮ“Ľ£ļ![]() =5.5(m)£¨
=5.5(m)£¨
Ļ īūįłő™£ļ5.5£Ľ
»őőŮ∂Ģ£ļ”…Ő‚“‚Ņ…Ķ√£ļňńĪŖ–őACDB£¨ňńĪŖ–őACEH∂ľ «ĺō–ő£¨
°ŗEH=AC=1.5£¨CD=AB=5.5£¨
…ŤEG=x m£¨
‘ŕRt°ųDEG÷–£¨°ŌDEC=90°„£¨°ŌGDE=31°„£¨
°Ŗtan31°„=![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨
‘ŕRt°ųCEG÷–£¨°ŌCEG=90°„£¨°ŌGCE=25.7°„£¨
°Ŗtan25.7°„=![]() £¨°ŗCE=
£¨°ŗCE=![]() £¨
£¨
°ŖCD=CE-DE£¨
°ŗ![]() £¨
£¨
°ŗ![]() £¨
£¨
°ŗGH=CE+EH=13.2+1.5=14.7£¨
īū£ļ∆žłňGHĶńłŖ∂»ő™14.7m£Ľ
»őőŮ»ż£ļīūįł≤Ľő®“Ľ£ļ√Ľ”–Őę—ŰĻ‚£¨∆žłňĶ◊≤Ņ≤ĽŅ…ĶĹīÔ£¨≤‚ŃŅ∆žłň”į◊”Ķń≥§∂»”ŲĶĹņßń—Ķ».

 ‘ń∂ŃŅž≥ĶŌĶŃ–īūįł
‘ń∂ŃŅž≥ĶŌĶŃ–īūįł