Question

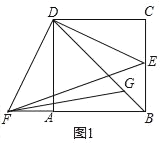
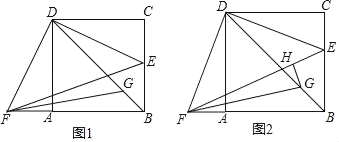
【题目】如图1，在正方形ABCD中，E是BC边上一点，F是BA延长线上一点，AF＝CE，连接BD，EF，FG平分∠BFE交BD于点G．

（1）求证：△ADF≌△CDE；

（2）求证：DF＝DG；

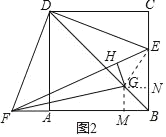
（3）如图2，若GH⊥EF于点H，且EH＝FH，设正方形ABCD的边长为x，GH＝y，求y与x之间的关系式．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3），理由详见解析.

【解析】

（1）根据SAS即可证明；
（2）欲证明DF=DG，只要证明∠DFG=∠DGF；
（3）如图2中，作GM⊥AB于M，GN⊥BC于N．连接EG．首先说明G是△BEF的内心，由题意Rt△FGH≌Rt△FGM，Rt△EGH≌Rt△EGN，四边形GMBN是正方形，推出FH=FM，EH=EN，GN=GM=BM=BN=y，由EH：FH=1：3，设EH=a，则FH=3a，FB=3a+y，BE=a+y，EC=AF，推出FB+BE=2x，可得3a+y+a+y=2x，即y=x-2a，推出CN=2a，推出CE=a，想办法用a表示x、y即可解决问题；

（1）证明：如图1中，∵四边形ABCD是正方形，

∴∠C＝∠BAD＝∠DAF＝90°，CD＝DA，

在△ADF和△CDE中，

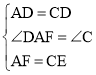
∴△ADF≌△CDE．

（2）证明：如图1中，∵四边形ABCD是正方形，

∴∠FBG＝45°，

∵△ADF≌△CDE，

∴DF＝DE，∠ADF＝∠CDE，

∴∠EDF＝∠ADC＝90°，

∠DFE＝45°，

∵∠DFG＝45°+∠EFG，∠DGF＝45°+∠GFB，

∵∠EFG＝∠BFG，

∴∠DFG＝∠DGF，

∴DF＝DG．

（3）结论：

理由：如图2中，作GM⊥AB于M，GN⊥BC于N．连接EG．

∵GF平分∠BAE，DB平分∠EBF，

∴G是△BEF的内心，∵GH⊥EF，

∴GH＝GN＝GM＝y，

∵FG＝FG，EG＝EG，

∴Rt△FGH≌Rt△FGM，Rt△EGH≌Rt△EGN，四边形GMBN是正方形，

∴FH＝FM，EH＝EN，GN＝GM＝BM＝BN＝y，

∵EH：FH＝1：3，设EH＝a，则FH＝3a，

∵FB＝3a+y，BE＝a+y，

∵EC＝AF，

∴FB+BE＝2x，

∴3a+y+a+y＝2x，

∴y＝x﹣2a，

∴CN＝2a，

∵EN＝EH＝a，

∴CE＝a，

在Rt△DEF中，DE＝2a，

在Rt△DCE中，

∴

∴