题目内容
求方程3x2-4x+k=0的两实根之积的最大值．
【答案】分析：根据根的判别式求出k的范围，根据根与系数的关系求出方程3x2-4x+k=0的两实根之积，把k的最大值代入求出即可．
解答：解：要使方程有两根，必须b2-4ac=（-4）2-4×3×k≥0，
解得：k≤
，
即k的最大值是
∵3x2-4x+k=0的两个之积是
，
∴
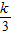的最大值是
=
．
答：方程3x2-4x+k=0的两实根之积的最大值是
．
点评：本题考查了根与系数的关系和根的判别式的应用，关键是求出k的最大值．
解答：解：要使方程有两根，必须b2-4ac=（-4）2-4×3×k≥0，
解得：k≤
，即k的最大值是
∵3x2-4x+k=0的两个之积是
，∴
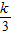的最大值是=．答：方程3x2-4x+k=0的两实根之积的最大值是
．点评：本题考查了根与系数的关系和根的判别式的应用，关键是求出k的最大值．
练习册系列答案
相关题目