题目内容
如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).

(1)求这个二次函数的关系式;
(2)若一次函数y=- x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
【答案】
(1)这个二次函数的关系式为y=(x-2)2+1;(2)当n=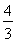 时,DQ取得最小值,为
时,DQ取得最小值,为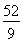 .
.
【解析】
试题分析:(1)由于顶点为M(2,1),故设这个二次函数的关系式为y=a(x-2)2+1,又因为过点N(3,2),代入解析式即可求出a的值,从而得到解析式;
(2)用含有n 得代数式表示出P,Q坐标,求出PQ最小值,再证得△DPQ∽△OAB,根据相似三角形性质即可求得DQ的最小值.
试题解析:(1)设这个二次函数的关系式为y=a(x-2)2+1.
把x=3,y=2代入得a+1=2,∴a=1.
∴这个二次函数的关系式为y=(x-2)2+1.
(2)由题意知P(n,n2-4n+5),Q(n,-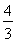 n-4).
n-4).
∴PQ=n2-4n+5-(-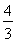 n-4)=n2-
n-4)=n2-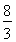 n+9=(n-
n+9=(n-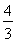 )2+
)2+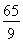 .?
.?
∴当n=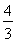 时,PQ取得最小值,为
时,PQ取得最小值,为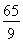 .
.
易证△DPQ∽△OAB,
∴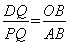 ,
,
∵一次函数y=-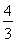 x-4的图象与x轴交于点A,与y轴交于点B,
x-4的图象与x轴交于点A,与y轴交于点B,
∴OB=4,OA=3,AB=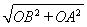 =5
=5
∴DQ= PQ=
PQ=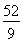 .
.
∴当n=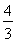 时,DQ取得最小值,为
时,DQ取得最小值,为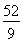 .
.
考点:二次函数与一次函数综合.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
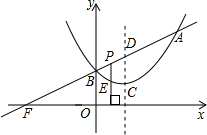 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.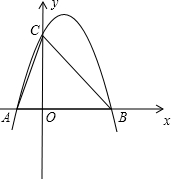
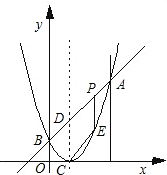 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.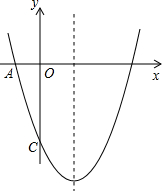 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).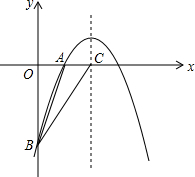 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数