题目内容
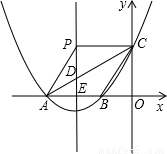
如图,已知抛物线y=ax2+4ax+t(a>0)交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0).(1)求抛物线的对称轴及点A的坐标;
(2)过点C作x轴的平行线交抛物线的对称轴于点P,你能判断四边形ABCP是什么四边形?并证明你的结论;
(3)连接CA与抛物线的对称轴交于点D,当∠APD=∠ACP时,求抛物线的解析式.
【答案】分析:(1)抛物线的对称轴为x=-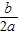 ,由此可求出抛物线的对称轴方程,由于A、B关于抛物线的对称轴对称,因此可根据B点的坐标求出A点的坐标.
,由此可求出抛物线的对称轴方程,由于A、B关于抛物线的对称轴对称,因此可根据B点的坐标求出A点的坐标.
(2)已知了CP∥AB,只需证CP是否与AB相等即可,根据抛物线对称轴x=-2可知CP=2,根据A、B的坐标不难得出AB=2,因此AB与PC平行且相等,四边形ABCP是平行四边形.
(3)本题的关键是求出C点的坐标,即OC的长,当∠APD=∠ACP时,△ADE∽△PAE,可得出AE2=DE•PE①,AE的长可根据A点坐标和抛物线的对称轴方程求得,而关键是求出DE、PE的比例关系,由于PE=OC,在相似三角形ADE和ACO中,可求出DE与OC的比例关系,也就求出了DE与PE的比例关系,然后将这个式子代入①中即可求出OC的长,已知了A、B、C三点坐标后可用待定系数法求出抛物线的解析式.
解答:解:(1)x=-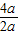 =-2,
=-2,
∴抛物线的对称轴是直线x=-2
设点A的坐标为(x,0),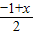 =-2,
=-2,
∴x=-3,A的坐标(-3,0)
(2)四边形ABCP是平行四边形
∵CP=2,AB=2,
∴CP=AB
又∵CP∥AB
∴四边形ABCP是平行四边形
(3)通过△ADE∽△CDP得出DE:PE=1:3
∵四边形ABCP是平行四边形
∴AB∥PC,
∴∠ACP=∠CAB,
∵∠APD=∠ACP,
∴∠APD=∠CAB,
∵∠AED是公共角,
∴△ADE∽△PAE,
∴12= •t
•t
解得t=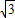 ,
,
将B(-1,0)代入抛物线y=ax2+4ax+t,
得t=3a,a=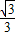 ,
,
抛物线的解析式为y=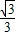 x2+
x2+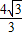 x+
x+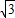 .
.
点评:该题综合性较强,它将二次函数和相似三角形、平行四边形贯穿在一起,考查综合分析问题能力,既考查二次函数的对称轴解析式,又考查相似三角形的性质和平行四边形的识别,是一个考查学生综合解题能力的好题.
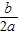 ,由此可求出抛物线的对称轴方程,由于A、B关于抛物线的对称轴对称,因此可根据B点的坐标求出A点的坐标.
,由此可求出抛物线的对称轴方程,由于A、B关于抛物线的对称轴对称,因此可根据B点的坐标求出A点的坐标.(2)已知了CP∥AB,只需证CP是否与AB相等即可,根据抛物线对称轴x=-2可知CP=2,根据A、B的坐标不难得出AB=2,因此AB与PC平行且相等,四边形ABCP是平行四边形.
(3)本题的关键是求出C点的坐标,即OC的长,当∠APD=∠ACP时,△ADE∽△PAE,可得出AE2=DE•PE①,AE的长可根据A点坐标和抛物线的对称轴方程求得,而关键是求出DE、PE的比例关系,由于PE=OC,在相似三角形ADE和ACO中,可求出DE与OC的比例关系,也就求出了DE与PE的比例关系,然后将这个式子代入①中即可求出OC的长,已知了A、B、C三点坐标后可用待定系数法求出抛物线的解析式.
解答:解:(1)x=-
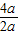 =-2,
=-2,∴抛物线的对称轴是直线x=-2
设点A的坐标为(x,0),
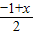 =-2,
=-2,∴x=-3,A的坐标(-3,0)
(2)四边形ABCP是平行四边形
∵CP=2,AB=2,
∴CP=AB
又∵CP∥AB
∴四边形ABCP是平行四边形
(3)通过△ADE∽△CDP得出DE:PE=1:3
∵四边形ABCP是平行四边形
∴AB∥PC,
∴∠ACP=∠CAB,
∵∠APD=∠ACP,
∴∠APD=∠CAB,
∵∠AED是公共角,
∴△ADE∽△PAE,
∴12=
 •t
•t解得t=
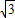 ,
,将B(-1,0)代入抛物线y=ax2+4ax+t,
得t=3a,a=
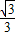 ,
,抛物线的解析式为y=
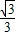 x2+
x2+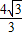 x+
x+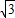 .
.点评:该题综合性较强,它将二次函数和相似三角形、平行四边形贯穿在一起,考查综合分析问题能力,既考查二次函数的对称轴解析式,又考查相似三角形的性质和平行四边形的识别,是一个考查学生综合解题能力的好题.

练习册系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;