题目内容
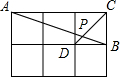 (2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是
(2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是2
2
.分析:首先连接BE,由题意易得BF=CF,△ACP∽△BDP,然后由相似三角形的对应边成比例,易得DP:CP=1:3,即可得PF:CF=PF:BF=1:2,在Rt△PBF中,即可求得tan∠BPF的值,继而求得答案.
解答: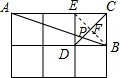 解:如图,连接BE,
解:如图,连接BE,
∵四边形BCED是正方形,
∴DF=CF=
CD,BF=
BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=
CF=
BF,
在Rt△PBF中,tan∠BPF=
=2,
∵∠APD=∠BPF,
∴tan∠APD=2.
故答案为:2.
 解:如图,连接BE,
解:如图,连接BE,∵四边形BCED是正方形,
∴DF=CF=
| 1 |
| 2 |
| 1 |
| 2 |
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PBF中,tan∠BPF=
| BF |
| PF |
∵∠APD=∠BPF,
∴tan∠APD=2.
故答案为:2.
点评:此题考查了相似三角形的判定与性质与三角函数的定义.此题难度适中,解题的关键准确作出辅助线,注意转化思想与数形结合思想的应用.

练习册系列答案
相关题目
 (2012•泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(2012•泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2. (2012•泰州)如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是
(2012•泰州)如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是 (2012•泰州)如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是
(2012•泰州)如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是 O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.