题目内容
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交DC于点F.(1)如图1,点G在矩形ABCD内部,试判断GF与DF的数量关系,并证明你的结论;
(2)①如图2,当点G在BC边上时,即有
| DC |
| DF |
| AD |
| AB |
②当点G在矩形ABCD内部时,如果
| DC |
| DF |
| AD |
| AB |
③当点G在矩形ABCD内部时,如果
| DC |
| DF |
| AD |
| AB |
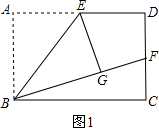
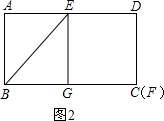
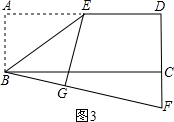
分析:(1)利用图形的翻折变换性质的出Rt△EGF≌Rt△EDF;
(2)运用(1)中结论得出
=2,进而利用射影定理表示出EG以及AD,AB的长求出即可.
(2)运用(1)中结论得出
| AD |
| AB |
解答: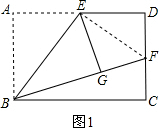 解:(1)GF=DF,
解:(1)GF=DF,
证明:∵矩形ABCD中,E是AD的中点,
将△ABE沿BE折叠后得到△GBE,
∴AE=DE,AE=EG,
EF=EF,∠A=∠BGE=∠D=90°,
∴Rt△EGF≌Rt△EDF,
∴FG=DF;
(2)①∵DC=DF,AE=ED=AB,
∴
=2,
故答案为:2;
②假设DF=x,则FG=x,BG=2x,
∵由(1)知∠BEF=90°,
∴EG2=BG×GF,
∴EG=
x,
AD=2
x,
AB=2x,
∴
=
;
③
,当点G在矩形ABCD外部时,得出的结论还成立.
 解:(1)GF=DF,
解:(1)GF=DF,证明:∵矩形ABCD中,E是AD的中点,
将△ABE沿BE折叠后得到△GBE,
∴AE=DE,AE=EG,
EF=EF,∠A=∠BGE=∠D=90°,
∴Rt△EGF≌Rt△EDF,
∴FG=DF;
(2)①∵DC=DF,AE=ED=AB,
∴
| AD |
| AB |
故答案为:2;
②假设DF=x,则FG=x,BG=2x,
∵由(1)知∠BEF=90°,

∴EG2=BG×GF,
∴EG=
| 2 |
AD=2
| 2 |
AB=2x,
∴
| AD |
| AB |
| 2 |
③
2
| ||
| t |
点评:此题主要考查了图形的翻折变换以及三角形全等的证明等几何基本知识,解题时应分别对每一个图形进行仔细分析,难度不大.

练习册系列答案
相关题目
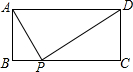 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
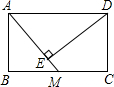 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为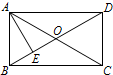 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为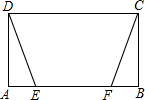 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.