题目内容
（2008•怀柔区二模）已知如图，矩形ABCD中，AB=3cm，BC=4cm，E是边AD上一点，且BE=ED，P是对角线上任意一点，PF⊥BE，PG⊥AD，垂足分别为F、G．则PF+PG的长为3
3
cm．分析：首先过点P作PM⊥BC于M，由矩形ABCD中，PG⊥AD，易证得G，P，M共线，且四边形ABMG是矩形，可得GM=AB=3cm，又由BE=ED，易证得∠EBD=∠CBD，然后根据角平分线的性质，可得PF=PM，继而可得PF+PG的长即为GM的长．
解答：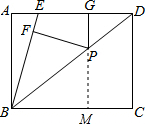
解：过点P作PM⊥BC于M，
∵四边形ABCD是矩形，
∴AD∥BC，∠A=∠ABC=90°，
∴PM⊥AD，
∵PG⊥AD，
∴G，P，M共线，
∴∠GMC=90°，
∴四边形ABMG是矩形，
∴GM=AB=3cm，
∵BE=ED，
∴∠EDB=∠EBD，
∵AD∥BC，
∴∠EDB=∠CBD，
∴∠EBD=∠CBD，
∵PF⊥BE，PM⊥BC，
∴PM=PF，
∴PF+PG=PM+PG=GM=3cm．
故答案为：3．
解：过点P作PM⊥BC于M，∵四边形ABCD是矩形，
∴AD∥BC，∠A=∠ABC=90°，
∴PM⊥AD，
∵PG⊥AD，
∴G，P，M共线，
∴∠GMC=90°，
∴四边形ABMG是矩形，
∴GM=AB=3cm，
∵BE=ED，
∴∠EDB=∠EBD，
∵AD∥BC，
∴∠EDB=∠CBD，
∴∠EBD=∠CBD，
∵PF⊥BE，PM⊥BC，
∴PM=PF，
∴PF+PG=PM+PG=GM=3cm．
故答案为：3．
点评：此题考查了矩形的性质、垂线的性质、等腰三角形的性质、平行线的性质以及角平分线的性质等知识．此题综合性较强，难度适中，解题的关键是准确作出辅助线，掌握数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
（2008•怀柔区二模）如图⊙O的直径AB与弦AC的夹角为30°，切线CD与AB的延长线交于点D．若⊙O的半径为3，则CD的长为