Question

如图所示，已知△ABC≌△ADE，BC的延长线交DE于F，∠B=∠D=25°，∠ACB=∠AED=105°，∠DAC=10°，则∠DFB为

1. A.
   40°
2. B.
   50°
3. C.
   55°
4. D.
   60°

Answer 1

D
分析：设AD与BF交于点M，要求∠DFB的大小，可以在△DFM中利用三角形的内角和定理求解，转化为求∠AMC的大小，再转化为在△ACM中求∠ACM就可以．
解答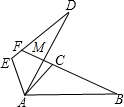：解：设AD与BF交于点M，
∵∠ACB=105，
∴∠ACM=180°-105°=75°，
∠AMC=180°-∠ACM-∠DAC=180°-75°-10°=95°，
∴∠FMD=∠AMC=95°，
∴∠DFB=180°-∠D-∠FMD=180°-95°-25°=60°．
故选D．
点评：本题考查了全等三角形的性质，由已知条件，联想到所学的定理，充分挖掘题目中的结论是解题的关键．