��Ŀ����
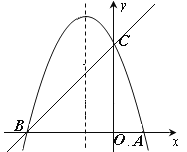
����Ŀ����1���۲�����ɣ�����ͼ1��ʾ��ƽ��ֱ������ϵ�У�ֱ��l��y��ƽ�У���M���N ��ֱ��l�ϵ����㣨��M�ڵ�N���Ϸ�����
���������֣�����M����Ϊ��2��3������N����Ϊ��2����4������MN�ij���Ϊ_____�� �������������ȡl�ϵ�����������ɳ������Ľ��ۣ�����M����Ϊ��t��m������N����Ϊ��t��n������m��nʱ��MN�ij��ȿɱ�ʾΪ______��
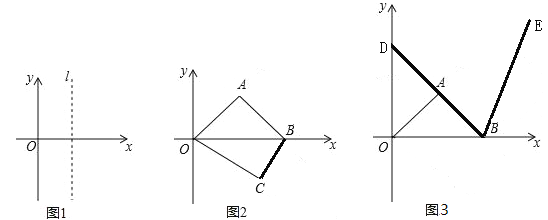
��2����ͼ2���ı���OABC�Ķ���O������ԭ�㣬��A�ڵ�һ���ޣ�![]() OAB=90
OAB=90![]() ��OA=AB����C�ڵ������ޣ�B�������Ϊ��6��0������OC=5����P���߶�OB�ϵ�һ�����㣨��P�����0��B�غϣ�������P����y��ƽ�е�ֱ��l�����P������Ϊt��
��OA=AB����C�ڵ������ޣ�B�������Ϊ��6��0������OC=5����P���߶�OB�ϵ�һ�����㣨��P�����0��B�غϣ�������P����y��ƽ�е�ֱ��l�����P������Ϊt��
����֪��t=4ʱ��ֱ��lǡ�þ�����C�����A��C��������ꣻ
���ڢٵ������£�ֱ��l����һ��M����MB=![]() OCʱ��ֱ��д�����������ĵ�M���ꣻ
OCʱ��ֱ��д�����������ĵ�M���ꣻ
����ͼ3�ӳ��߶�BA��y���ڵ�D���߶�BD˳ʱ����ת60![]() ��D��Ķ�Ӧ��Ϊ��E���Ƿ�� ��x���ϵĵ�Q,ʹ��QD+QE��ֵ��С���������������Q�����꣬�����
��D��Ķ�Ӧ��Ϊ��E���Ƿ�� ��x���ϵĵ�Q,ʹ��QD+QE��ֵ��С���������������Q�����꣬�����![]() OQD�Ķ����� �������ڣ���˵������.
OQD�Ķ����� �������ڣ���˵������.
���𰸡� ��1��7 m-n;(2)��A(3,3), C(4,-3),��M(4,![]() )��(4,-
)��(4,-![]() ); �۴��ڣ�Q(
); �۴��ڣ�Q(![]() ,0)��
,0)��![]() OQD=600
OQD=600
�������������������1��ֱ��l��y��ƽ�У�M��x1��y1����N��x2��y2����M��N�����������ȣ��ٸ���AB�ij���Ϊ|y1��y2|������ã�
(2) �ٹ�A����AE![]() OB�ڵ�E,��ֱ�����������߹�ϵ�ó���A��C�����ꣻ��ֱ�ӵó����ɣ�������QD��BF,����ֱ�������κͽ�ֱ��������
OB�ڵ�E,��ֱ�����������߹�ϵ�ó���A��C�����ꣻ��ֱ�ӵó����ɣ�������QD��BF,����ֱ�������κͽ�ֱ��������
�����������1���� 7 �� m-n
(2)��ͼ2. �ٹ�A����AE![]() OB�ڵ�E,
OB�ڵ�E,

![]()
![]() OAB=900,OA=AB ,B(6,0),AE
OAB=900,OA=AB ,B(6,0),AE![]() OB
OB
��OE=AE=BE=![]() OB=3,
OB=3, ![]() AOB=
AOB=![]() AOB= 450,A(3,3).
AOB= 450,A(3,3).
��Rt![]() OPC��OC=5,OP=4,��PC=3,
OPC��OC=5,OP=4,��PC=3,
��C(4,-3)
��M(4,![]() )��(4,-
)��(4,-![]() )
)
����ͼ3.��D�����x��ĶԳƵ�Ϊ��F,����EF��x���ڵ�Q,

����QD��BF,��![]() DBO=
DBO=![]() FBO=
FBO= ![]() BDO=
BDO=![]() BFO= 450,BD=BF,
BFO= 450,BD=BF,
OD=OB=6,![]() DBF=900.
DBF=900.
![]()
![]() DBE=600,BD=BE,
DBE=600,BD=BE,![]() DBF=900,
DBF=900,
��![]() FBE=1500,BE=BF,
FBE=1500,BE=BF,![]() BFE=150,
BFE=150,![]() QFO=300,
QFO=300,
�ɶԳƿ�֪��![]() QFO=
QFO=![]() QDO=300,��
QDO=300,��![]() OQD=600.
OQD=600.
��OQ=x,��DQ=2x
��Rt![]() ODQ��
ODQ�У�![]()
![]()
��![]()
��x=![]()
�� Q(![]() ,0)
,0)