Question

如图，A、B是反比例函数y=

k

x

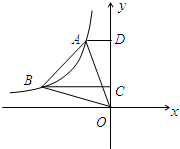图象上的两点，过A、B两点分别作y轴的垂线，垂足为D、C，且AD=1，BC=3，∠ABC=45°．
（1）求反比例函数的解析式；
（2）求三角形OAB的面积．

Answer 1

分析：（1）本题需先根据已知条件，得出A、B的坐标，再把它的坐标代入即可得出k的值，最后求出反比例函数的解析式．
（2）本题需先求出S_梯形ABCD+S_△BOC-S_△AOD的值，即可得出三角形OAB的面积．

解答：解：（1）∵AD=1，
∴点A的坐标为（-1，-k），
∵BC=3
∴点B的坐标为（-3，-

k

3

)，
∴-k-（-

k

3

）=2
解得：k=-3，
∴反比例函数的解析式是；y=-

3

x

；

（2）三角形OAB的面积=S_梯形ABCD+S_△BOC-S_△AOD，
=

(1+3)×2

2

+

3

2

-

3

2

，
=4．

点评：本题主要考查了反比例函数综合题，在解题时要能根据题意列出式子求出结果是本题的关键．