题目内容
【题目】已知：在平面直角坐标系中，点
和点
分别在
轴和
轴的正半轴上，
的平分线与正比例函数
交于点
，且与
相交于点
，在轴负半轴上有一点
.
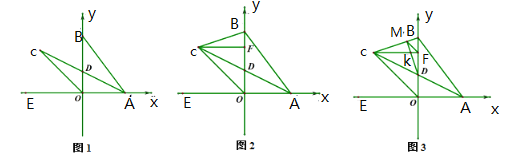
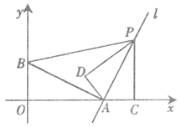
（1）如图1，求证：
；
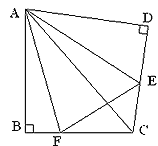
（2）如图2，过点作
，垂足为
，连接
，求证：
；
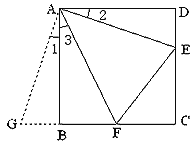
（3）如图3，在（2）的条件下，过点作
，垂足为点
，交
于点
，连接
，若
，
，求直线
的解析式.
【答案】（1）见解析；（2）见解析；（3）
.
【解析】
（1）根据平行线的性质及角平分线的定义，通过角的运算得出
；
（2）如图所示作辅助线，根据已知条件，得出四边形
为正方形，再根据角平分线的定义及全等三角形的性质得出
；
（3）如图所示作辅助线，通过辅助线及等量代换，得出
，进而得出
为等腰直角三角形，得出
，再通过
，设出未知数，表达出，根据已知条件及勾股定理，列出方程，解出A，B坐标，进而求出一次函数的解析式.
（1）如图1，∵
平分
∴
∵正比例函数
的图象是直线
∴
∵
∴
∵
∴
∴
（2）如图2，过点
作
，垂足为点
，过点作
，垂足为点
.
∵
∴
∴四边形为矩形
∵
∴
∴
∴四边形为正方形
∴
∵是
的角平分线
∴
∵
∴
∵
，
∴
∴
∵
，
∴
∴
∵
∴
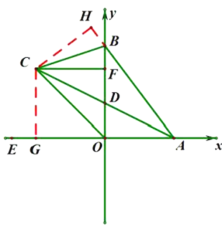
（3）如图3，延长
到点，由（2）问可得
平分
，
∵平分
∴由（1）问的方法可得
∵
∴
为等腰直角三角形
即
过点
作
交
于点
，
∵
，
，
∴
∵
，
，
∴
∴
∴
，
即为等腰直角三角形
∴
∵
∴
∵，
，
∴设
，
∴
，
，
，
，
∵
，
∴
由（2）可知
设
，则
，即
，
在
中
∴
即
，
设直线的解析式为
解得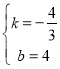
，.
练习册系列答案
小学期末标准试卷系列答案
相关题目
