题目内容

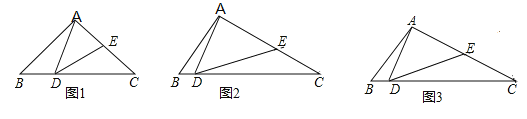
【题目】如图，在正三角形ABC中，点D、E分别在AC、AB上，且，AE=BE，则有（ ）

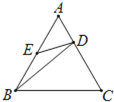
A.△AED∽△BEDB.△AED∽△CBD

C.△AED∽△ABDD.△BAD∽△BCD

【答案】B

【解析】

本题可以采用排除法，即根据已知中正三角形ABC中，D、E分别在AC、AB上，，AE=BE，我们可以分别得到：△AED、△BCD为锐角三角形，△BED、△ABD为钝角三角形，然后根据锐角三角形不可能与钝角三角形相似排除错误答案，得到正确答案．

由已知中正三角形ABC中，D、E分别在AC、AB上，，AE=BE，
易判断出：△AED为一个锐角三角形，△BED为一个钝角三角形，故A错误；
△ABD也是一个钝角三角形，故C也错误；
但△BCD为一个锐角三角形，故D也错误；
故选：B．

练习册系列答案
相关题目

【题目】如图是一种雪球夹的简化结构图，其通过一个固定夹体和一个活动夹体的配合巧妙地完成夹雪、投雪的操作，不需人手直接接触雪，使用方便，深受小朋友的喜爱．当雪球夹闭合时，测得∠AOB＝30°，OA＝OB＝14 cm，则此款雪球夹制作的雪球的直径AB的长度为________ cm．(结果保留一位小数．参考数据：sin15°≈0．26，cos15°≈0．97，tan15°≈0．27)

【题目】（1）问题发现

如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．

填空：

①∠AEB的度数为　 　；

②线段AD，BE之间的数量关系为　 　．

（2）拓展探究

如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．

（3）解决问题

如图3，在正方形ABCD中，CD=3，若点P满足PD=1，且∠BPD=90°，请直接写出点A到BP的距离．

【题目】如图，一次函数的图象与反比例函数的图象相交于A（2，1），B两点．

（1）求出反比例函数与一次函数的表达式；

（2）请直接写出B点的坐标，并指出使反比例函数值大于一次函数值的x的取值范围．

【题目】“淮南牛肉汤”是安徽知名地方小吃．某分店经理发现，当每碗牛肉汤的售价为6元时，每天能卖出500碗；当每碗牛肉汤的售价每增加0.5元时，每天就会少卖出20碗，设每碗牛肉汤的售价增加元时，一天的营业额为元．

（1）求与的函数关系式（不要求写出的取值范围）；

（2）考虑到顾客可接受价格元/碗的范围是，且为整数，不考虑其他因素，则该分店的牛肉汤每碗多少元时，每天的牛肉汤营业额最大？最大营业额是多少元？

【题目】在中，点为上一点，点为上一点，且．

(1)如图1，若，求证：；

(2)如图2，若，求证：；

(3) 如图3，在(2)的条件下，若，且，，直接写出线段的长．

【题目】某竹制品加工厂根据市场调研结果，对该厂生产的一种新型竹制品玩具未来两年的销售进行预测，并建立如下模型：设第t个月，竹制品销售量为P（单位：箱），P与t之间存在如图所示函数关系，其图象是线段AB（不含点A）和线段BC的组合．设第t个月销售每箱的毛利润为Q（百元），且Q与t满足如下关系Q=2t+8（0≤t≤24）．

（1）求P与t的函数关系式（6≤t≤24）．

（2）该厂在第几个月能够获得最大毛利润？最大毛利润是多少？

（3）经调查发现，当月毛利润不低于40000且不高于43200元时，该月产品原材料供给和市场售最和谐，此时称这个月为“和谐月”，那么，在未来两年中第几个月为和谐月？

【题目】如图，已知∠AOB=90°，点A绕点O顺时针旋转后的对应点A1落在射线OB上，点A绕点A1顺时针旋转后的对应点A2落在射线OB上，点A绕点A2顺时针旋转后的对应点A3落在射线OB上，…，连接AA1，AA2，AA3…，依此作法，则∠AA2A3=___，∠AAnAn+1等于___度．（用含n的代数式表示，n为正整数）．

【题目】如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE∥BA交AC于点E，DF∥CA交AB于点F，已知CD=3．

（1）求AD的长；

（2）求四边形AEDF的周长．（注意：本题中的计算过程和结果均保留根号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网