ΧβΡΩΡΎ»ί
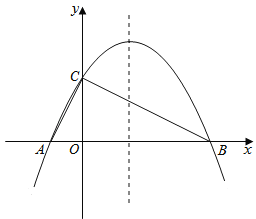
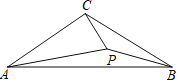
ΓΨΧβΡΩΓΩΡ≥÷ώ÷ΤΤΖΦ”ΙΛ≥ßΗυΨί –≥ΓΒς―–ΫαΙϊΘ§Ε‘ΗΟ≥ß…ζ≤ζΒΡ“Μ÷÷–¬–Ά÷ώ÷ΤΤΖΆφΨΏΈ¥ά¥ΝΫΡξΒΡœζ έΫχ––‘Λ≤βΘ§≤ΔΫ®ΝΔ»γœ¬ΡΘ–ΆΘΚ…ηΒΎtΗω‘¬Θ§÷ώ÷ΤΤΖœζ έΝΩΈΣPΘ®ΒΞΈΜΘΚœδΘ©Θ§P”κt÷°Φδ¥φ‘Ύ»γΆΦΥυ ΨΚ· ΐΙΊœΒΘ§ΤδΆΦœσ «œΏΕΈABΘ®≤ΜΚ§ΒψAΘ©ΚΆœΏΕΈBCΒΡΉιΚœΘ°…ηΒΎtΗω‘¬œζ έΟΩœδΒΡΟΪάϊ»σΈΣQΘ®ΑΌ‘ΣΘ©Θ§«“Q”κt¬ζΉψ»γœ¬ΙΊœΒQ=2t+8Θ®0ΓήtΓή24Θ©Θ°
Θ®1Θ©«σP”κtΒΡΚ· ΐΙΊœΒ ΫΘ®6ΓήtΓή24Θ©Θ°
Θ®2Θ©ΗΟ≥ß‘ΎΒΎΦΗΗω‘¬ΡήΙΜΜώΒΟΉν¥σΟΪάϊ»σΘΩΉν¥σΟΪάϊ»σ «Εύ…ΌΘΩ
Θ®3Θ©Ψ≠Βς≤ιΖΔœ÷Θ§Β±‘¬ΟΪάϊ»σ≤ΜΒΆ”Ύ40000«“≤ΜΗΏ”Ύ43200‘Σ ±Θ§ΗΟ‘¬≤ζΤΖ‘≠≤ΡΝœΙ©ΗχΚΆ –≥Γ έΉνΚΆ–≥Θ§¥Υ ±≥Τ’βΗω‘¬ΈΣΓΑΚΆ–≥‘¬Γ±Θ§Ρ«Ο¥Θ§‘ΎΈ¥ά¥ΝΫΡξ÷–ΒΎΦΗΗω‘¬ΈΣΚΆ–≥‘¬ΘΩ

ΓΨ¥πΑΗΓΩΘ®1Θ©PΘΫ©¹t+26Θ®6ΓήtΓή24Θ©ΘΜΘ®2Θ©ΗΟ≥ß‘ΎΒΎ11Ηω‘¬ΡήΙΜΜώΒΟΉν¥σΟΪάϊ»σΘ§Ήν¥σΟΪάϊ»σ «45000‘ΣΘΜΘ®3Θ©Έ¥ά¥ΝΫΡξ÷–ΒΡΚΆ–≥‘¬”–ΘΚ6Θ§7Θ§8Θ§14Θ§15Θ§16’βΝυΗω‘¬Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Β±6ΓήtΓή24 ±Θ§…ηP”κtΒΡΚ· ΐΙΊœΒ ΫΈΣP=kt+bΘ§Α―ΒψBΘ®6Θ§20Θ©ΚΆCΘ®24Θ§2Θ©¥ζ»κ«σ≥ωkΚΆbΘ§Φ¥Ω…ΒΟΫβΘΜ
Θ®2Θ©…η÷±œΏABΒΡΚ· ΐΫβΈω ΫΈΣP=mt+nΘ§ΫΪAΘ®0Θ§14Θ©Θ§B Θ®6Θ§20Θ©¥ζ»κ«σ≥ωmΚΆnΘ§Ζ÷0ΘΦtΘΦ6ΚΆ6ΓήtΓή24ά¥Χ÷¬έ«σΫβΘΜ
Θ®3Θ©Ζ÷0ΘΦtΘΦ6ΚΆ6ΓήtΓή24Θ§ΫαΚœΘ®2Θ©÷–«σΒΟΒΡΟΪάϊ»σΚ· ΐΘ§Ν–≤ΜΒ» ΫΉιΩ…ΫβΘ°
Θ®1Θ©Β±6ΓήtΓή24 ±Θ§…ηP”κtΒΡΚ· ΐΙΊœΒ ΫΈΣP=kt+bΘ°
ΓΏΗΟΆΦœσΙΐΒψBΘ®6Θ§20Θ©ΚΆCΘ®24Θ§2Θ©Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύP”κtΒΡΚ· ΐΙΊœΒ ΫΈΣP=©¹t+26Θ®6ΓήtΓή24Θ©Θ°
Θ®2Θ©…η÷±œΏABΒΡΚ· ΐΫβΈω ΫΈΣP=mt+nΘ§ΫΪAΘ®0Θ§14Θ©Θ§B Θ®6Θ§20Θ©¥ζ»κΒΟΘΚ
![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ÷±œΏABΒΡΚ· ΐΫβΈω ΫΈΣP=t+14Θ§
ΓύΒ±0ΘΦtΘΦ6 ±Θ§άϊ»σL=QP=Θ®2t+8Θ©Θ®t+14Θ©=2t2+36t+112=2Θ®t+9Θ©2©¹50Θ°
Β±t=5 ±Θ§άϊ»σL»ΓΉν¥σ÷ΒΈΣ2Θ®5+9Θ©2©¹50=342Θ®ΑΌ‘ΣΘ©=34200Θ®‘ΣΘ©ΘΜ
Β±6ΓήtΓή24 ±Θ§άϊ»σL=QP=Θ®2t+8Θ©Θ®©¹t+26Θ©=©¹2t2+44t+208=©¹2Θ®t©¹11Θ©2+450Θ°
450ΑΌ‘Σ=45000‘ΣΘ§
ΓύΒ±t=11 ±Θ§άϊ»σL”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ45000‘ΣΘ°
Ήέ…œΥυ ωΘΚΗΟ≥ß‘ΎΒΎ11Ηω‘¬ΡήΙΜΜώΒΟΉν¥σΟΪάϊ»σΘ§Ήν¥σΟΪάϊ»σ «45000‘ΣΘ°
Θ®3Θ©ΓΏ40000‘Σ=400ΑΌ‘ΣΘ§43200‘Σ=432ΑΌ‘ΣΘ§
Γύ![]() Μρ
Μρ![]()
ΒΎ“ΜΗω≤ΜΒ» ΫΈόΫβΘ§ΒΎΕΰΗω≤ΜΒ» ΫΒΡΫβΈΣ6ΓήtΓή8Μρ14ΓήtΓή16Θ§
ΓύΈ¥ά¥ΝΫΡξ÷–ΒΡΚΆ–≥‘¬”–ΘΚ6Θ§7Θ§8Θ§14Θ§15Θ§16’βΝυΗω‘¬Θ°