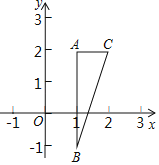ЬтФПФкШн
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
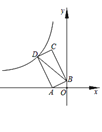
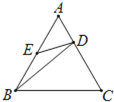
ШчЭМ1ЃЌЁїACBКЭЁїDCEОљЮЊЕШБпШ§НЧаЮЃЌЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯЃЌСЌНгBEЃЎ
ЬюПеЃК
ЂйЁЯAEBЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЂкЯпЖЮADЃЌBEжЎМфЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭиеЙЬНОП
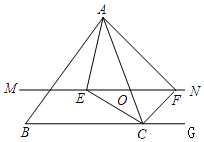
ШчЭМ2ЃЌЁїACBКЭЁїDCEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯDCE=90ЁуЃЌЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯЃЌCMЮЊЁїDCEжаDEБпЩЯЕФИпЃЌСЌНгBEЃЌЧыХаЖЯЁЯAEBЕФЖШЪ§МАЯпЖЮCMЃЌAEЃЌBEжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
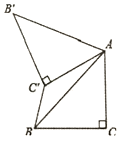
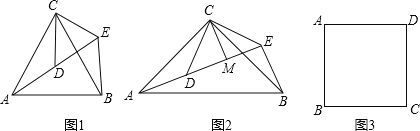
ШчЭМ3ЃЌдке§ЗНаЮABCDжаЃЌCD=3ЃЌШєЕуPТњзуPD=1ЃЌЧвЁЯBPD=90ЁуЃЌЧыжБНгаДГіЕуAЕНBPЕФОрРыЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй60ЁуЃЛЂкAD=BEЃЛЃЈ2ЃЉЁЯAEB=90ЁуЃЌAE=BE+2CMЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬѕМўвзжЄЁїACDЁеЁїBCEЃЌДгЖјЕУЕНЃКAD=BEЃЌЁЯADC=ЁЯBECЃЎгЩЕуAЃЌDЃЌEдкЭЌвЛжБЯпЩЯПЩЧѓГіЁЯADCЃЌДгЖјПЩвдЧѓГіЁЯAEBЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЗТееЃЈ1ЃЉжаЕФНтЗЈПЩЧѓГіЁЯAEBЕФЖШЪ§ЃЌжЄГіAD=BEЃЛгЩЁїDCEЮЊЕШбќжБНЧШ§НЧаЮМАCMЮЊЁїDCEжаDEБпЩЯЕФИпПЩЕУCM=DM=MEЃЌДгЖјжЄЕНAE=2CH+BEЃЎ
ЃЈ3ЃЉгЩPD=1ПЩЕУЃКЕуPдквдЕуDЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯЃЛгЩЁЯBPD=90ЁуПЩЕУЃКЕуPдквдBDЮЊжБОЖЕФдВЩЯЃЎЯдШЛЃЌЕуPЪЧетСНИідВЕФНЛЕуЃЌгЩгкСНдВгаСНИіНЛЕуЃЌНгЯТРДашЖдСНИіЮЛжУЗжБ№НјааЬжТлЃЎШЛКѓЃЌЬэМгЪЪЕБЕФИЈжњЯпЃЌНшжњгкЃЈ2ЃЉжаЕФНсТлМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉ![]() ЁЯACB=ЁЯDCEЃЌЁЯDCB=ЁЯDCB
ЁЯACB=ЁЯDCEЃЌЁЯDCB=ЁЯDCB
![]() ЁЯACD=ЁЯBCE
ЁЯACD=ЁЯBCE
дкЁїACDКЭЁїBCEжа
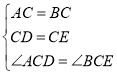
![]()
![]() AD=BEЃЌЁЯCEB=ЁЯADC=180Ёу-ЁЯCDE=120Ёу
AD=BEЃЌЁЯCEB=ЁЯADC=180Ёу-ЁЯCDE=120Ёу
![]() ЁЯAEB=ЁЯCEB-ЁЯCED=60Ёу.
ЁЯAEB=ЁЯCEB-ЁЯCED=60Ёу.
ЂкЁпЁїACDЁеЁїBCEЃЌЁрAD=BEЃЎД№АИЮЊЃКAD=BEЃЎ
ЃЈ2ЃЉЁЯAEB=90ЁуЃЌAE=BE+2CMЃЎ
РэгЩЃКШчЭМ 2ЃЌ
ЁпЁїACB КЭЁїDCE ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCA=CBЃЌCD=CEЃЌЁЯACB=ЁЯDCE=90ЁуЃЎ
ЁрЁЯACD=ЁЯBCEЃЎ
дкЁїACD КЭЁїBCE жаЃЌ
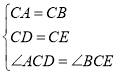
ЁрЁїACDЁеЁїBCEЃЎЁрAD=BEЃЌЁЯADC=ЁЯBECЃЎ
ЁпЁїDCE ЮЊЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯCDE=ЁЯCED=45ЁуЃЎ
ЁпЕу AЃЌDЃЌE дкЭЌвЛжБЯпЩЯЃЌЁрЁЯADC=135ЁуЃЎ
ЁрЁЯBEC=135ЁуЃЎЁрЁЯAEB=ЁЯBECЉЁЯCED=90ЁуЃЎ
ЁпCD=CEЃЌCMЁЭDEЃЌЁрDM=MEЃЎ
ЁпЁЯDCE=90ЁуЃЌЁрDM=ME=CMЃЎ
ЁрAE=AD+DE=BE+2CMЃЎ
ЃЈ3ЃЉЕуAЕНBPЕФОрРыЮЊ![]() Лђ
Лђ![]()
РэгЩШчЯТЃК
ЁпPD=1ЃЌ
ЁрЕуPдквдЕуDЮЊдВаФЃЌ1ЮЊАыОЖЕФдВЩЯЁЃ
ЁпЁЯBPD=90ЃЌ
ЁрЕуPдквдBDЮЊжБОЖЕФдВЩЯЁЃ
ЁрЕуPЪЧетСНдВЕФНЛЕуЁЃ
ЂйЕБЕуPдкШчЭМ3ЂйЫљЪОЮЛжУЪБЃЌ
СЌНгPDЁЂPBЁЂPA,зїAHЁЭBP,ДЙзуЮЊH,
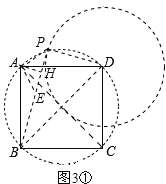
Й§ЕуAзїAEЁЭAPЃЌНЛBPгкЕуEЃЌШчЭМ3ЂйЁЃ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯADB=45.AB=AD=DC=BC=3,ЁЯBAD=90.
ЁрBD=2.
ЁпDP=1ЃЌ
ЁрBP=![]() .
.
ЁпЁЯBPD=ЁЯBAD=90ЃЌ
ЁрAЁЂPЁЂD. BдквдBDЮЊжБОЖЕФдВЩЯЃЌ
ЁрЁЯAPB=ЁЯADB=45.
ЁрЁїPAEЪЧЕШбќжБНЧШ§НЧаЮЁЃ
гжЁпЁїBADЪЧЕШбќжБНЧШ§НЧаЮЃЌЕуB. E. PЙВЯпЃЌAHЁЭBPЃЌ
ЁргЩ(2)жаЕФНсТлПЩЕУЃКBP=2AH+PD.
Ёр![]() =2AH+1.
=2AH+1.
ЁрAH=![]() .
.
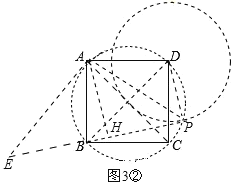
ЂкЕБЕуPдкШчЭМ3ЂкЫљЪОЮЛжУЪБЃЌ
СЌНгPDЁЂPBЁЂPAЃЌзїAHЁЭBPЃЌДЙзуЮЊHЃЌ
Й§ЕуAзїAEЁЭAPЃЌНЛPBЕФбгГЄЯпгкЕуEЃЌШчЭМ3ЂкЁЃ
ЭЌРэПЩЕУЃКBP=2AHPD.
Ёр![]() =2AH1.
=2AH1.
ЁрAH=![]() .
.
злЩЯЫљЪіЃКЕуAЕНBPЕФОрРыЮЊ![]() Лђ
Лђ![]() .
.