题目内容
 在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上.
在△ABC中,∠ACB=90°,点A的坐标为(0,2),点B(-3,1)在抛物线y=ax2+ax-2上,点C在x轴上.
(1)求a的值;
(2)求点C的坐标;
(3)若△ABC是等腰直角三角形
①如图1,将△ABC绕顶点A逆时针方向旋转β°(0<β<180°)得到△AB′C′,当点C′(2,1)恰好落在该抛物线上,请你通过计算说明点B′也在该抛物线上.
②如图2,设抛物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,若P、Q两点的运动速度相同,请问谁先到达点B,为什么?
解:(1)∵点B(-3,1)在抛物线y=ax2+ax-2上,
∴1=9a-3a-2,
∴a= ;
;
(2)过B作BE⊥x轴,垂足为E,设OC=a,则CE=OE-OC=3-x,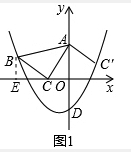
∴∠BEC=∠AOC=90°,
∴∠BCE+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCE=∠CAO,
∴△BEC∽△COA,
∴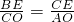 ,
,
即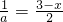 ,
,
整理得:a2-3a+2=0,
解得:a=1或2,
∴点C的坐标是(-1,0)或(-2,0);
(3)若△ABC是等腰直角三角形,则C的坐标是(-1,0),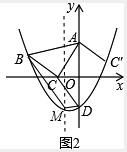
①将△ABC绕顶点A逆时针方向旋转β°(0<β<180°)得到△AB′C′,则AC=AC′= ,CC′=
,CC′= ,∠CAC′=90°,
,∠CAC′=90°,
∴点B′的坐标是(1,-1),
把(1,-1)代入y= x2+
x2+ x-2得:
x-2得: ×1+
×1+ ×1-2=-1,
×1-2=-1,
∴点B′也在该抛物线上;
②设抛物线的顶点M,
∵y= x2+
x2+ x-2=
x-2= (x+
(x+ )2-
)2-
∴M点的坐标为(- ,-
,- ),
),
∴DC+BC=2 ≈4.42,DM+MB=
≈4.42,DM+MB=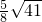 +
+
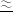 4.517,
4.517,
∴DC+BC<DM+MB,
∵P、Q两点的运动速度相同,
∴P点先到达点B.
分析:(1)把点B的坐标(-3,1)代入二次函数的解析式y=ax2+ax-2即可求出a的值;
(2)过B作BE⊥x轴,垂足为E,设OC=a,证明△BEC∽△COA,利用相似三角形的性质:对应边的比值相等得到根据a的方程解方程求出a的值即可;
(3)①若△ABC是等腰直角三角形,则点C的坐标为(-1,0),将△ABC绕顶点A逆时针方向旋转β°(0<β<180°)得到△AB′C′,则AC=AC′= ,CC′=
,CC′= ,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(-
,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(- ,-
,- ),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2
),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2 ,DM+MB=
,DM+MB=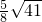 +
+ ,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.
,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.
点评:此题主要考查了二次函数解析式的确定、相似三角形的判定和性质、坐标系两点间的距离公式等重要知识;(3)题中,由于Q点的移动轨迹是条曲线,在求其移动距离时,能够通过辅助线来化曲为直,间接的得出P、Q的路程大小是解决问题的关键.
∴1=9a-3a-2,
∴a=
 ;
;(2)过B作BE⊥x轴,垂足为E,设OC=a,则CE=OE-OC=3-x,

∴∠BEC=∠AOC=90°,
∴∠BCE+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCE=∠CAO,
∴△BEC∽△COA,
∴
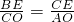 ,
,即
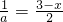 ,
,整理得:a2-3a+2=0,
解得:a=1或2,
∴点C的坐标是(-1,0)或(-2,0);
(3)若△ABC是等腰直角三角形,则C的坐标是(-1,0),

①将△ABC绕顶点A逆时针方向旋转β°(0<β<180°)得到△AB′C′,则AC=AC′=
 ,CC′=
,CC′= ,∠CAC′=90°,
,∠CAC′=90°,∴点B′的坐标是(1,-1),
把(1,-1)代入y=
 x2+
x2+ x-2得:
x-2得: ×1+
×1+ ×1-2=-1,
×1-2=-1,∴点B′也在该抛物线上;
②设抛物线的顶点M,
∵y=
 x2+
x2+ x-2=
x-2= (x+
(x+ )2-
)2-
∴M点的坐标为(-
 ,-
,- ),
),∴DC+BC=2
 ≈4.42,DM+MB=
≈4.42,DM+MB=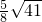 +
+
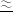 4.517,
4.517,∴DC+BC<DM+MB,
∵P、Q两点的运动速度相同,
∴P点先到达点B.
分析:(1)把点B的坐标(-3,1)代入二次函数的解析式y=ax2+ax-2即可求出a的值;
(2)过B作BE⊥x轴,垂足为E,设OC=a,证明△BEC∽△COA,利用相似三角形的性质:对应边的比值相等得到根据a的方程解方程求出a的值即可;
(3)①若△ABC是等腰直角三角形,则点C的坐标为(-1,0),将△ABC绕顶点A逆时针方向旋转β°(0<β<180°)得到△AB′C′,则AC=AC′=
 ,CC′=
,CC′= ,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(-
,∠CAC′=90°,进而求出B′的坐标,代入函数的解析式验证即可;②由抛物线的解析式可求出顶点M坐标(- ,-
,- ),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2
),物线与y轴的交点为D、P、Q两点同时从D点出发,点P沿折线D→C→B运动到点B,点Q沿抛物线(在第二、三象限的部分)运动到点B,则DC+BC=2 ,DM+MB=
,DM+MB=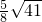 +
+ ,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.
,因为P、Q两点的运动速度相同再比较DC+BC和DM+MB的大小即可知道谁先到达点B.点评:此题主要考查了二次函数解析式的确定、相似三角形的判定和性质、坐标系两点间的距离公式等重要知识;(3)题中,由于Q点的移动轨迹是条曲线,在求其移动距离时,能够通过辅助线来化曲为直,间接的得出P、Q的路程大小是解决问题的关键.

练习册系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
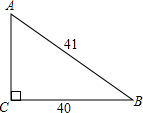 如图,在△ABC中,AC=
如图,在△ABC中,AC= 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=