Question

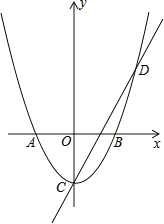
【题目】如图，在平面直角坐标系中，抛物线与x轴交于点A（﹣1，0）和点B（1，0），直线y=2x﹣1与y轴交于点C，与抛物线交于点C、D．

（1）求抛物线的解析式；

（2）求点A到直线CD的距离；

（3）平移抛物线，使抛物线的顶点P在直线CD上，抛物线与直线CD的另一个交点为Q，点G在y轴正半轴上，当以G、P、Q三点为顶点的三角形为等腰直角三角形时，求出所有符合条件的G点的坐标．

Answer 1

【答案】（1）抛物线的解析式为：y=x2﹣1．（2）点A到直线CD的距离为．（3）符合条件的点G有两个，其坐标为（0，4）或（0，9）．

【解析】

试题分析：（1）首先求出点C坐标，然后利用待定系数法求出抛物线的解析式；

（2）设直线CD与x轴交于点E，求出点E的坐标，然后解直角三角形（或利用三角形相似），求出点A到直线CD的距离；

（3）△GPQ为等腰直角三角形，有三种情形，需要分类讨论．为方便分析与计算，首先需要求出线段PQ的长度．

方法一：

解：（1）直线y=2x﹣1，当x=0时，y=﹣1，则点C坐标为（0，﹣1）．

设抛物线解析式为y=ax2+bx+c，

∵点A（﹣1，0）、B（1，0）、C（0，﹣1）在抛物线上，

∴，

解得，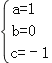

∴抛物线的解析式为：y=x2﹣1．

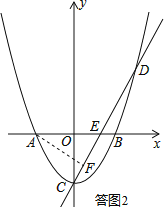
（2）如答图2所示，直线y=2x﹣1，

当y=0时，x=；

设直线CD交x轴于点E，则E（，0）．

在Rt△OCE中，OC=1，OE=，

由勾股定理得：CE=，

设∠OEC=θ，则sinθ=，cosθ=．

过点A作AF⊥CD于点F，

则AF=AEsinθ=（OA+OE）sinθ=（1+）×=，

∴点A到直线CD的距离为．

（3）∵平移后抛物线的顶点P在直线y=2x﹣1上，

∴设P（t，2t﹣1），则平移后抛物线的解析式为y=（x﹣t）2+2t﹣1．

联立，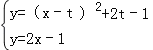

化简得：x2﹣（2t+2）x+t2+2t=0，

解得：x1=t，x2=t+2，

即点P、点Q的横坐标相差2，

∴PQ===．

△GPQ为等腰直角三角形，可能有以下情形：

i）若点P为直角顶点，如答图3①所示，

则PG=PQ=．

∴CG====10，

∴OG=CG﹣OC=10﹣1=9，

∴G（0，9）；

ii）若点Q为直角顶点，如答图3②所示，

则QG=PQ=．

同理可得：G（0，9）；

iii）若点G为直角顶点，如答图3③所示，

此时PQ=，

则GP=GQ=．

分别过点P、Q作y轴的垂线，垂足分别为点M、N．

易证Rt△PMG≌Rt△GNQ，

∴GN=PM，GM=QN．

在Rt△QNG中，

由勾股定理得：GN2+QN2=GQ2，

即PM2+QN2=10 ①

∵点P、Q横坐标相差2，

∴NQ=PM+2，

代入①式得：PM2+（PM+2）2=10，

解得PM=1，

∴NQ=3．

直线y=2x﹣1，

当x=1时，y=1，

∴P（1，1），

即OM=1．

∴OG=OM+GM=OM+NQ=1+3=4，

∴G（0，4）．

综上所述，符合条件的点G有两个，其坐标为（0，4）或（0，9）．

方法二：

（1）略．

（2）作AF⊥CD，垂足为F，∴KCD×KAF=﹣1，

∵KCD=2，∴KAF=﹣，

∵A（﹣1，0），∴lAF：y=﹣x﹣，

∵lCD：y=2x﹣1，

∴lAF与lCD的交点坐标F（，﹣），

∴AF=．

（3）∵平移后抛物线的顶点P在直线y=2x﹣1上，设P（t，2t﹣1），

则平移后抛物线的解析式为y=（x﹣t）2+2t﹣1，

∴抛物线与直线的交点P（t，2t﹣1），Q（t+2，2t+3），

以G、P、Q三点为顶点的三角形为等腰直角三角形．

①点G可视为点Q绕点P逆时针旋转90°而成，将P点平移至原点P′（0，0），

则Q′（2，4），将Q′点绕原点逆时针旋转90°，则G′（﹣4，2），

将P′平移至P点，则G′平移后即为G（﹣4+t，2t+1），

∵GX=0，∴t=4，∴G1（0，9），

②同理可得G2（0，9），

③点P可视为点Q绕点G顺时针旋转90°而成，设G（0，b），

将G平移至原点，G′（0，0），则Q′（t+2，2t+3﹣b），

将Q′绕原点顺时针旋转90°，则P′（2t+3﹣b，﹣t﹣2），

将G′平移至G点，则P′平移后即为P（2t+3﹣b，﹣t﹣2+b），

∴2t+3﹣b=t，﹣t﹣2+b=2t﹣1，∴t=1，b=4，

∴G3（0，4），

综上所述，满足题意的点G1（0，9），G2（0，4）．