题目内容
如果方程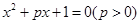
有实数根且它的两根之差是1，那么p的值为
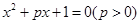有实数根且它的两根之差是1，那么p的值为| A．2 | B．4 | C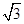． | D． |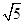
D
分析：先根据判别式求出p的取值范围，再根据根与系数的关系即可得出答案．
解答：解：由△=p2-4＞0及p＞2，设x1，x2为方程的两根，
那么有x1+x2=-p，x1x2=l，
又由（x1-x2）2=（x1+x2）2-4x1x2，
得：1=（-p）2-4，
解得：p2=5，
∴p=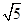
（p＞2）．
故选D．
解答：解：由△=p2-4＞0及p＞2，设x1，x2为方程的两根，
那么有x1+x2=-p，x1x2=l，
又由（x1-x2）2=（x1+x2）2-4x1x2，
得：1=（-p）2-4，
解得：p2=5，
∴p=
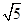（p＞2）．故选D．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
的根（ ）
，
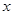的一元二次方程
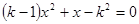的一个根为1，则
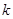的值为 
的方程
是一元二次方程，则
＝