题目内容
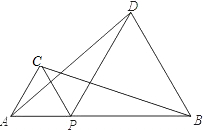 如图,P为AB上一点,△APC和△BPD是等边三角形,AD和BC相等吗?如果相等,写出证明过程,若不相等,说明理由.
如图,P为AB上一点,△APC和△BPD是等边三角形,AD和BC相等吗?如果相等,写出证明过程,若不相等,说明理由.
分析:等边三角形各边长相等,则AP=CP,PB=PD,证明∠APD=∠BPC即可求证△APD≌△BPC,即可求证AD=BC.
解答:解:相等.
理由:∵△APC和△BPD是等边三角形,
∴AP=CP,PB=PD,
∵∠APD=∠APC+∠CPD,∠CPB=∠CPD+∠BPD,∠APC=∠BPD=60°,
∴∠APD=∠CPB,
∴
,
∴△APD≌△CPB(SAS),
∴AD=BC.
理由:∵△APC和△BPD是等边三角形,
∴AP=CP,PB=PD,
∵∠APD=∠APC+∠CPD,∠CPB=∠CPD+∠BPD,∠APC=∠BPD=60°,
∴∠APD=∠CPB,
∴
|
∴△APD≌△CPB(SAS),
∴AD=BC.
点评:本题考查了全等三角形的证明,全等三角形对应边相等的性质,等边三角形边长相等、各内角为60°的性质,本题中求证△APD≌△CPB是解题的关键.

练习册系列答案
相关题目
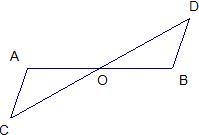 12、如图,O为AB上一点,要使△AOC与△BOD全等,还需满足条件
12、如图,O为AB上一点,要使△AOC与△BOD全等,还需满足条件 (2009•郑州模拟)如图,C为AB上一点,点D、E分别在AB的两侧,AC=BE,BC=AD,请探索当AD和BE有何位置关系时,CD和EC相等?说明你的理由.
(2009•郑州模拟)如图,C为AB上一点,点D、E分别在AB的两侧,AC=BE,BC=AD,请探索当AD和BE有何位置关系时,CD和EC相等?说明你的理由.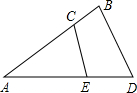 如图,C为AB上一点,E为AD上一点,且AB•AC=AD•AE
如图,C为AB上一点,E为AD上一点,且AB•AC=AD•AE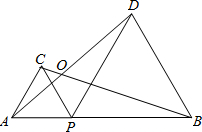 如图,P为AB上一点,△APC和△BPD是等边三角形,AD与BC相交于O
如图,P为AB上一点,△APC和△BPD是等边三角形,AD与BC相交于O