题目内容
如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).

(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.

(1)探究DB′与EC′的数量关系,并给予证明;
(2)当DB′∥AE时,试求旋转角α的度数.
(1)DB′=EC′,见解析 (2)60°
解:(1)DB′=EC′.理由如下:
∵AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点,
∴AD=AE=
 AB,∵△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′,
AB,∵△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′,∴∠B′AD=∠C′AE=a,AB′=AB,AC′=AC,∴AB′=AC′,
在△B′AD和C′AE中,
∵
 ∴
∴ ≌
≌
∴DB′=EC′;
(2)∵DB′∥AE,∴∠B′DA=∠DAE=90°,
在Rt△B′DA中,
∵AD=
 AB=
AB= AB′,
AB′,∴∠AB′D=30°,∴∠B′AD=90°-30°=60°,
即旋转角α的度数为60°.

练习册系列答案
相关题目
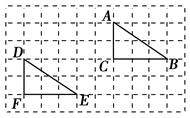
 的三个顶点的位置如图所示,现将△
的三个顶点的位置如图所示,现将△ 对应点
对应点 ,点
,点 分别对应点
分别对应点 .
. .
. ,则这两条线段之间的关系是__ __.
,则这两条线段之间的关系是__ __.