题目内容
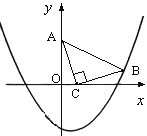
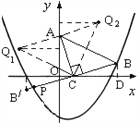
【题目】如图，在直角坐标系中，已知点A（0, 3）、点C（1, 0），等腰Rt△ACB的顶点B在抛物线
上.
（1）求点B的坐标及抛物线的解析式；
（2）在抛物线上是否存在点P（点B除外），使△ACP是以AC为直角边的Rt△？若存在，求出所有点P的坐标；若不存在，请说明理由.
（3）在抛物线上是否存在点Q（点B除外），使△ACQ是以AC为直角边的等腰Rt△？若存在直接写出所有点Q的坐标；若不存在，请说明理由.
【答案】（1）
（2）P2（
、 P3（
（3）不存在.
【解析】试题分析：（1）首先过点B作BD⊥x轴，垂足为D，易证得△BDC≌△COA，即可得BD=OC=1，CD=OA=2，则可求得点B的坐标；（2）利用待定系数法即可求得二次函数的解析式；（3）分别从①以AC为直角边，点C为直角顶点，则延长BC至点P1使得P1C=BC，得到等腰直角三角形ACP1，过点P1作P1M⊥x轴，②若以AC为直角边，点A为直角顶点，则过点A作AP2⊥CA，且使得AP2=AC，得到等腰直角三角形ACP2，过点P2作P2N⊥y轴，③若以AC为直角边，点A为直角顶点，则过点A作AP3⊥CA，且使得AP3=AC，得到等腰直角三角形ACP3，过点P3作P3H⊥y轴，去分析则可求得答案．
试题解析:
（1）过B作BD⊥x轴，则△AOC≌△CDB，
∴B（4，1）
将B（4，1）代入
得： 
（2）以C为直角顶点时P是BC与
的交点,
BC的解析式为
; 解得P1（－1，－ 
）（其中点B舍去）
以A为直角顶点时，过A的直线平行于BC，∴易得解析式为
, 与抛物线交点：
P2（
、 P3（
（3）不存在
理由：以C为直角顶点时，点B关于AC的对称点B/(―2,―1)不满足抛物线解析式
以A为直角顶点时，令AQ1＝AC，求得Q1(―3，2) 不满足抛物线解析式
同理，当AQ2＝AC时，求得Q2（3，4）不满足抛物线解析式
