题目内容
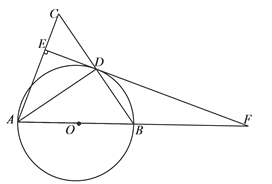
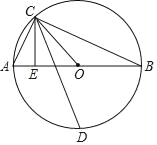
【题目】如图AB为⊙O的直径,C为⊙O上半圆的一个动点,CE⊥AB于点E,∠OCE的角平分线交⊙O于D点.
(1)当C点在⊙O上半圆移动时,D点位置会变吗?请说明理由;
(2)若⊙O的半径为5,弦AC的长为6,连接AD,求线段AD、CD的长.
【答案】(1)当C点在⊙O上半圆移动时,D点位置不会变;理由见解析;(2)线段AD的长度为5![]() ,线段CD的长度为7
,线段CD的长度为7![]() .
.
【解析】
(1)连接OD.根据角平分线的性质得到∠1=∠3,根据原点半径相等得到OC=OD,根据等边对等角得到∠1=∠2,等量代换得到∠2=∠3,即可判定CE∥OD,
又CE⊥AB,则OD⊥AB,根据垂径定理可知点D为半圆AB的中点.
(2)在直角△AOD中,OA=OD=5,根据勾股定理即可求出![]() 过点A作CD的垂线,垂足为G,根据圆周角定理得到
过点A作CD的垂线,垂足为G,根据圆周角定理得到![]() 即可求出
即可求出![]() 在直角△AGD中,
在直角△AGD中,![]() 即可求出CD的长.
即可求出CD的长.
(1)当C点在⊙O上半圆移动时,D点位置不会变;
理由如下:连接OD.
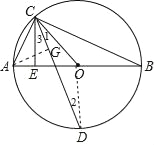
∵CD平分∠OCE,
∴∠1=∠3,
而OC=OD,
∴∠1=∠2,
∴∠2=∠3,
∴CE∥OD,
∵CE⊥AB,
∴OD⊥AB,
∴![]() =
=![]() ,即点D为半圆AB的中点.
,即点D为半圆AB的中点.
(2)∵在直角△AOD中,OA=OD=5,
∴![]()
过点A作CD的垂线,垂足为G,
∵![]()
∴△AGC是等腰直角三角形,
∵AC=6,
∴![]()
在直角△AGD中,![]()
∴![]()
∴线段AD的长度为![]() ,线段CD的长度为
,线段CD的长度为![]() .
.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目