题目内容
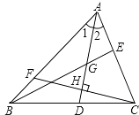
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=35°,以C为旅转中心,将△ABC旋转到△A′B′C的位置,点B在边A′B′上,则∠BDC为( )
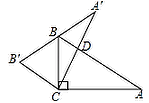
A.70°B.90°C.100°D.105°
【答案】D
【解析】
根据三角形内角和定理求出∠ABC,再由旋转的性质可知BC=B′C, ∠ABC=∠B′,从而求出∠BCB′,根据旋转角相等求出∠ACA′,最后根据外角定理即可求出∠BDC.
∵在Rt△ABC中,∠ACB=90°,∠A=35°,
∴∠ABC=90°-35°=55°,
由旋转的性质可知BC=B′C, ∠ABC=∠B′,∠BCB′=∠ACA′,
∴∠ABC=∠B′=∠B′BC=55°,
∴∠BCB′=180°-∠B′-∠B′BC=180°-55°-55°=70°,
∴∠ACA′=70°,
∴∠BDC=∠A+∠ACA′=35°+70°=105°.
故选D.

练习册系列答案
相关题目
【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
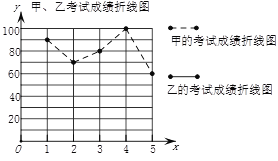
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)