题目内容
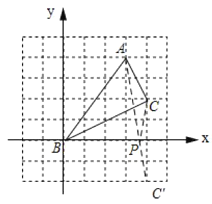
【题目】如图,在7×7网格中,每个小正方形边长都为1.建立适当的平面直角坐标系,使点A(3,4)、C(4,2).

(1)判断△ABC的形状,并求图中格点△ABC的面积;
(2)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值为__________.
【答案】(1)直角三角形,面积是5(2)![]()
【解析】
(1)首先根据A和C的坐标确定坐标轴的位置,然后确定B的坐标,再利用勾股定理的逆定理即可作出判断,再根据直角三角形的面积公式即可求解;
(2)作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC,依据轴对称图形的性质可得到PC=PC′,然后依据两点之间线段最短可知当点A,P,C′在一条直线上时,AP+PC有最小值.
(1)如图,建立直角坐标系,
∴B的坐标是(0,0).
∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,BC=![]() ,AC=
,AC=![]()
∴S△ABC=![]() BC×AC=
BC×AC=![]() ×
×![]() ×
×![]() =5;
=5;
(2)如图所示:作点C关于x轴的对称点C′连接AC′交x轴与点P,连接PC.
∵点C与点C′关于x轴对称,
∴PC=PC′.
∴AP+PC=AP+PC.
∴当A,P,C′在一条直线上时,AP+PC有最小值,最小值为AC′的长.
∵AC′=![]() .
.
∴AP+PC的最小值为![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】假如你的母亲开了一家服装店,专门卖羽绒服,下面是去年一年各月销售情况表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
销量(件) | 100 | 90 | 50 | 11 | 8 | 6 | 4 | 6 | 5 | 30 | 80 | 110 |
根据上表,回答下列问题:
(1)计算去年各季度的销售情况,并用一幅适当的统计图表示;
(2)计算去年各季度销售量在全年销售总量中所占的百分比,并用适当的统计图表示;
(3)从这些统计图表中,你能得出什么结论?为你母亲今后的决策能提供什么有用的帮助?