题目内容
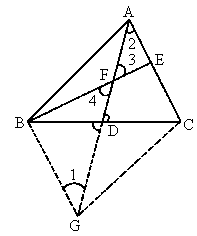
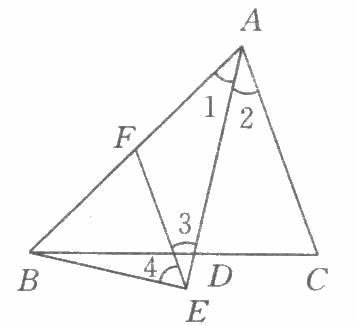
如图所示,AD⊥BF,AE⊥CF,垂足分别为D,E,且DF=EF,∠BAF=∠CAF,求证:∠B=∠C.

答案:
解析:
解析:
|
因为DF⊥AD,EF⊥AE,且DF=EF,所以∠DAF=∠EAF. 因为∠BAF=∠CAF,所以∠BAD=∠CAE.在Rt△ADF和Rt△AEF中, 因为AD⊥BF,AE⊥CF,所以∠ADB=∠AEC=90°. 在△ADB和△AEC中 所以∠B=∠C. |

练习册系列答案
相关题目
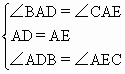 ,所以△ADB≌△AEC(ASA).
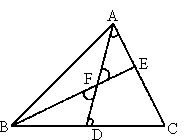
,所以△ADB≌△AEC(ASA).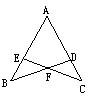 11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C.
11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C.