题目内容
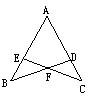 11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C.
11、(1)已知:如图所示,BD与EC交于F点,AD=AE,∠B=∠C.求证:①AB=AC;
②△EFB≌△DFC;
③BF=FC;
(2)如图所示,△ABD≌△ACE.求证:FE=FD.
分析:(1)分别证明△ABD≌△ACE和△EFB≌△DFC就能得到结论,
(2)由△ABD≌△ACE,可证AD=AE,AB=AC,∠B=∠C,进而证明BE=CD,然后证明△BEF≌△CDF,得到结论.
(2)由△ABD≌△ACE,可证AD=AE,AB=AC,∠B=∠C,进而证明BE=CD,然后证明△BEF≌△CDF,得到结论.
解答:证明:①∵AD=AE,∠B=∠C,
又∠A=∠A,
∴△ABD≌△ACE,
∴AB=AC;
②由①知AB=AC,
又AD=AE,
∴BE=DC,
又∠B=∠C,∠BFE=∠CFD,
∴△EFB≌△DFC;
③由②知△EFB≌△DFC,
∴BF=FC;
(2)∵△ABD≌△ACE,∴AD=AE,AB=AC,∠B=∠C,
∴AB-AE=AC-AD,即BE=CD,
在△BEF和△CDF中,∠B=∠C,∠BFE=∠CFD,BE=CD,
∴△BEF≌△CDF,
∴FE=FD.
又∠A=∠A,
∴△ABD≌△ACE,
∴AB=AC;
②由①知AB=AC,
又AD=AE,
∴BE=DC,
又∠B=∠C,∠BFE=∠CFD,
∴△EFB≌△DFC;
③由②知△EFB≌△DFC,
∴BF=FC;
(2)∵△ABD≌△ACE,∴AD=AE,AB=AC,∠B=∠C,
∴AB-AE=AC-AD,即BE=CD,
在△BEF和△CDF中,∠B=∠C,∠BFE=∠CFD,BE=CD,
∴△BEF≌△CDF,
∴FE=FD.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( ) 已知,如图所示,Rt△ABC的周长为4+2
已知,如图所示,Rt△ABC的周长为4+2 22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由.
22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由. 24、已知:如图所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
24、已知:如图所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由. 已知:如图所示,正比例函数y=ax的图象与反比例函数y=
已知:如图所示,正比例函数y=ax的图象与反比例函数y=