��Ŀ����
����Ŀ����ͼ1��������![]() ������A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱߡ�ABC��
������A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱߡ�ABC��
��1���������ߵĽ���ʽ��
��2����x���Ϸ������������Ƿ���ڵ�M����S��ABM=![]() S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
��3����ͼ2��E���߶�AC�ϵĶ��㣬F���߶�BC�ϵĶ��㣬AF��BE�ཻ�ڵ�P��
����CE=BF���Բ���AF��BE��������ϵ����APB�Ķ�������˵�����ɣ�
����AF=BE������E��A�˶���Cʱ����ֱ��д����P������·����������Ҫд���̣���

���𰸡���1��![]() ����2����M������Ϊ��9��4����1��4������3����AF=BE����APB=120�㣻��
����2����M������Ϊ��9��4����1��4������3����AF=BE����APB=120�㣻��![]() ��
��![]() ��
��
���������⣺��1���������⣬���������ߵĽ���ʽΪy=ax2+bx+![]() ��
��
�߽���A��B���������ã� 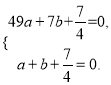 ��ã�a=
��ã�a=![]() ��b=��2��
��b=��2��
�������ߵĽ���ʽΪy=![]() x2��2x+
x2��2x+![]() ��
��
��2�����ڵ�M��ʹ��S��AMB=![]() S��ABC��
S��ABC��
���ɣ���ͼ��ʾ������C��CK��x�ᣬ����ΪK��
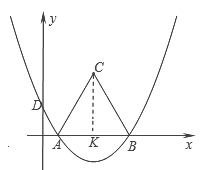
�ߡ�ABCΪ�ȱ������Σ�
��AB=BC=AC=6����ACB=60�㣮
��CK��AB��
��KA=BK=3����ACK=30�㣮
��CK=3![]() ��
��
��S��ABC=![]() ABCK=
ABCK=![]() ��6��3
��6��3![]() =9
=9![]() ��
��
��S��ABM=![]() ��
��![]() =12��
=12��
��M��a��![]() a2��2a+
a2��2a+![]() ����
����
��![]() AB|yM|=12����
AB|yM|=12����![]() ��6����
��6����![]() a2��2a
a2��2a![]() ��=12��
��=12��
���![]() =9��
=9�� ![]() =��1��
=��1��
��M1��9��4����M2����1��4����
��3���ٽ��ۣ�AF=BE����APB=120�㣮
���ɣ���ͼ��ʾ��
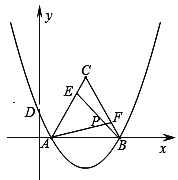
�ߡ�ABCΪ�ȱ������Σ�
��BC=AB����C=��ABF��
���ڡ�BEC�͡�AFB�У� 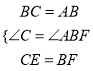 ��
��
���BEC�ա�AFB��
��AF=BE����CBE=��BAF��
���FAB+��ABP=��ABP+��CBE=��ABC=60�㣮
���APB=180�㩁��PAB����ABP=180�㩁60��=120�㣮
�ڵ�P������·����Ϊ![]() ��3
��3![]() ��
��

����Ŀ��ij�̳�Ͷ��13800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼۣ�Ԫ/�䣩 |
�� | 24 | 36 |
�� | 33 | 48 |
��1�����̳������ס������ֿ�Ȫˮ�������䣿
��2��ȫ������500���Ȫˮ�����̳�������������Ԫ��

