题目内容
【题目】如图所示，在
中
点C是OB的中点，D、E分别是直线AB、OA上的动点，则
周长的最小值是__________。
【答案】
【解析】
作点C关于AB的对称点F，关于AO的对称点G，连接DF，EG，由轴对称的性质，可得DF=DC，EC=EG，故当点F，D，E，G在同一直线上时，△CDE的周长=CD+DE+CE=DF+DE+EG=FG，此时△DEC周长最小，依据勾股定理即可得到FG的长，进而得到△CDE周长的最小值．
解：根据题意，如图，作点C关于AB的对称点F，关于AO的对称点G，连接DF，EG，
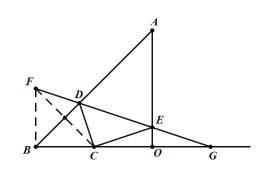
∵在
中
，点C是OB的中点，
∴BC=OC=OG=BF=1，
∴BG=3，∠FBC=45°+45°=90°，
由轴对称的性质，可得DF=DC，EC=EG，
当点F，D，E，G在同一直线上时，
∴△CDE的周长=CD+DE+CE=DF+DE+EG=FG，此时△DEC周长最小，
在
中，有
，
∴
；
∴△CDE周长的最小值为：；
故答案为：.
练习册系列答案
天天练口算系列答案
相关题目
