题目内容
【题目】在△ABC中,AC=BC,∠ACB=90°,D、E是直线AB上两点.∠DCE=45°
(1)当CE⊥AB时,点D与点A重合,求证:DE2=AD2+BE2
(2)当AB=4时,求点E到线段AC的最短距离
(3)当点D不与点A重合时,探究:DE2=AD2+BE2是否成立?若成立,请证明;若不成立,请说明理由

【答案】(1)证明见详解;(2)![]() ;(3)成立,证明见详解.
;(3)成立,证明见详解.
【解析】
(1)由等腰直角三角形的性质直接得出结果;
(2)当CE⊥AB时,点D与点A重合时,点E到AC的距离最短;过点E作EG⊥AC于点G,由等腰直角三角形的性质,得到AG=GE,然后利用勾股定理即可得到GE的长度;
(3)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答;
(1)解:如图:当CE⊥AB时,点D与点A重合,
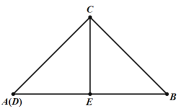
∵CE⊥AB,
∴AE=BE,
∵点D与点A重合,
∴DE=BE,
∴DE2=AD2+BE2;
(2)根据题意,当CE⊥AB时,点D与点A重合时,点E到AC的距离最短;
过点E作EG⊥AC于点G,如图:
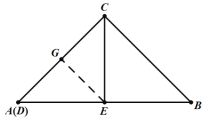
在等腰直角三角形ABC中,
∠A=45°,AE=BE=![]() ,
,
∴△AGE是等腰直角三角形,即AG=GE,
由勾股定理,得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴点E到线段AC的最短距离为:![]() ;
;
(3)![]() 成立;
成立;
证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
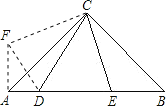
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,∠ACF=∠BCE,
∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵![]() ,
,
∴![]() ;
;