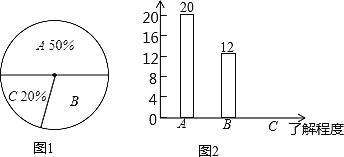
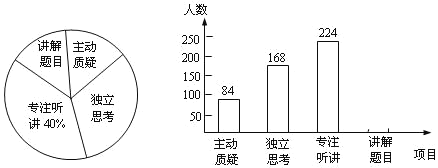
题目内容
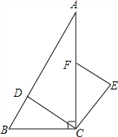
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
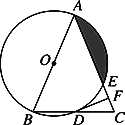
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
【答案】(1)详见解析;(2)4π-8.
【解析】试题分析:(1)连OD,AD,利用OD∥AC证明OD⊥DF.(2)利用扇形面积减去三角形面积求阴影部分面积.
试题解析:
(1)相切。证明:如图,连OD,AD,
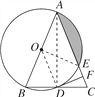
∵AB是⊙O的直径,∴AD⊥BC,
又∵AB=AC,∴D是BC的中点,
∵OA=OB∴OD是△ABC的中位线,
∴OD∥AC∵DF⊥AC, ∴OD⊥DF,
∴DF是⊙O的切线.
(2)解:∵∠CDF=22.5°,DF⊥AC,∴∠C=67.5°,
∴∠BAC=2∠DAC=45°,
连接OE,则∠BOE=2∠BAC=90°,∴∠AOE=90°,
∴S阴影=![]() ×4×4=4π-8.
×4×4=4π-8.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目