题目内容
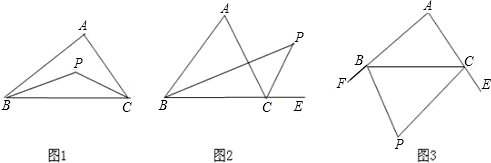
已知△ABC,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+ ∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°- ∠A.上述说法正确的个数是
∠A.上述说法正确的个数是
- A.0个
- B.1个
- C.2个
- D.3个
C
分析:用角平分线的性质和三角形内角和定理证明,证明时可运用反例.
解答:(1)若P点是∠ABC和∠ACB的角平分线的交点,
则∠PBC= ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB
∠ACB
则∠PBC+∠PCB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)
(180°-∠A)
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A,
∠A,
故成立;
(2)当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
(3)若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC= ∠FBC=
∠FBC= (180°-∠ABC)=90°-
(180°-∠ABC)=90°- ∠ABC,
∠ABC,
∠BCP= ∠BCE=90°-
∠BCE=90°- ∠ACB
∠ACB
∴∠PBC+∠BCP=180°- (∠ABC+∠ACB)
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°-∠A
∴∠PBC+∠BCP=90°+ ∠A,
∠A,
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180- (180°+∠A)=90°-
(180°+∠A)=90°- ∠A,
∠A,
故成立.
∴说法正确的个数是2个.
故选C.
点评:利用特例,反例可以比较容易的说明一个命题是假命题.
分析:用角平分线的性质和三角形内角和定理证明,证明时可运用反例.
解答:(1)若P点是∠ABC和∠ACB的角平分线的交点,
则∠PBC=
 ∠ABC,∠PCB=
∠ABC,∠PCB= ∠ACB
∠ACB则∠PBC+∠PCB=
 (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)
(180°-∠A)在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
 (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A,
∠A,故成立;
(2)当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
(3)若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC=
 ∠FBC=
∠FBC= (180°-∠ABC)=90°-
(180°-∠ABC)=90°- ∠ABC,
∠ABC,∠BCP=
 ∠BCE=90°-
∠BCE=90°- ∠ACB
∠ACB∴∠PBC+∠BCP=180°-
 (∠ABC+∠ACB)
(∠ABC+∠ACB)又∵∠ABC+∠ACB=180°-∠A
∴∠PBC+∠BCP=90°+
 ∠A,
∠A,在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
 (180°+∠A)=90°-
(180°+∠A)=90°- ∠A,
∠A,故成立.
∴说法正确的个数是2个.
故选C.
点评:利用特例,反例可以比较容易的说明一个命题是假命题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
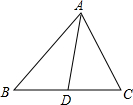 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
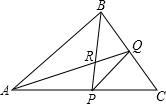 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于