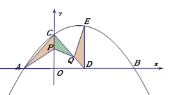Question

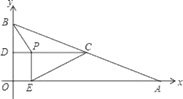
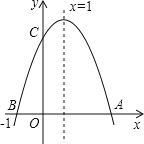
【题目】如图，直线y＝3x+3交x轴于A点，交y轴于B点，过A、B两点的抛物线交x轴于另一点C（3，0）．

（1）求A、B的坐标；

（2）求抛物线的解析式；

（3）在抛物线的对称轴上是否存在点Q，使△ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）A（﹣1，0），B（0，3）；（2）y＝﹣x2+2x+3；（3）存在，Q（1，1），（1，0），（1，），（1，﹣）．

【解析】

（1）已知一次函数解析式，分别令即可解决.

（2）设出抛物线的一般式，将三点坐标代入用待定系数法即可解决.

（3）抛物线解析式后可得其对称轴为，可设，此时需要分三种情况讨论：，每一种的线段长度用表示出来，列方程求解即可.

解：（1）∵y＝3x+3，

∴当x＝0时，y＝3，

当y＝0时，x＝﹣1，

∴A（﹣1，0），B（0，3）．

（2）设抛物线的解析式为，由题意，得

，

解得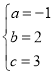

∴抛物线的解析式为：y＝﹣x2+2x+3.

（3）∵y＝﹣x2+2x+3，

∴y＝﹣（x﹣1）2+4

∴抛物线的对称轴为x＝1，设，

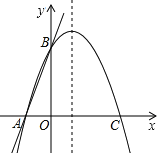
（1）当AQ＝BQ时，如图，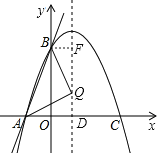

由勾股定理可得

BQ＝，

AQ＝

AQ＝BQ

即，

解得，

∴Q（1，1）；

（2）如图：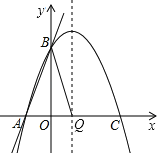

当AB是腰时，Q是对称轴与x轴交点时，AB＝BQ，

∴

解得：或6，

当Q点的坐标为（1，6）时，其在直线AB上，A、B和Q三点共线，舍去，

则此时Q的坐标是（1，0）；

（3）当AQ＝AB时，如图：

，

解得，

则Q的坐标是（1，）和（1，﹣）．

综上所述：Q（1，1），（1，0），（1，），（1，﹣）．