题目内容
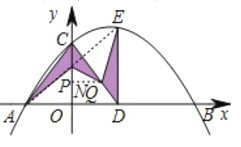
【题目】如图,抛物线![]() 与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
(1)若S1+S3=4S2 ,求Q点坐标;
(2)连结AQ,求AP+AQ的最小值;
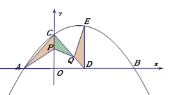
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先求出A,C的坐标,作QN∥OD,根据等腰三角形的性质得出D(3,0),进而求得E(3,5),根据勾股定理求得CD=5,设PC=QD=x,由△NQC∽△ODC的性质得出NQ=![]() ,根据S1+S3=4S2,列出关于x的方程,即可求得x的值,进而求得NQ和ON,就求得Q点的坐标;
,根据S1+S3=4S2,列出关于x的方程,即可求得x的值,进而求得NQ和ON,就求得Q点的坐标;
(2)连接AE,先证明△ACP≌△EQD,则AP=EQ,所以AP+AQ=EQ+AQ,利用三角形三边的关系得到EQ+AQ≥AE(当且仅当点A、Q、E共线时取等号),然后计算出AE即可.
(1)令![]() =0
=0
解得x1=-3,x2=8
∴A(-3,0),B(8,0)
令x=0,得y=4
∴C(0,4),
∵AC=CD,CO⊥AD,
∴OD=OA=3,
∴D(3,0),
∴E点的横坐标为3,
把x=3代入![]() 得,y=5,
得,y=5,
∴E(3,5),
∵OD=3,OC=4,
∴CD=5,
设PC=QD=x,
作QN∥OD,交OC于N,
∴△NQC∽△ODC,
∴![]() ,即
,即![]() ,
,
∴NQ=![]() ,
,
∵S1+S3=4S2,
∴![]() x3+
x3+![]() ×5[3
×5[3![]() ]=4
]=4![]() x
x![]()
解得x=![]() ,
,
∴QD=![]() ,
,
∵![]() ,
,
∴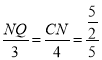 ,
,
∴NQ=![]() ,CN=2,
,CN=2,
∴ON=42=2,
∴Q(![]() ,2);
,2);
(2)连接AE,
∵AC=CD,CO⊥AD,
∴OC平分∠ACD,
∴∠ACO=∠DCO,
∵ED∥OC,
∴∠DCO=∠CDE,
∵DE=CD=AC=5,CP=QD,
∴△ACP≌△EDQ,
∴AP=EQ,
∴AP+AQ=EQ+AQ,
而EQ+AQ≥AE(当且仅当点A、Q、E共线时取等号),
∴EQ+AQ的最小值=![]() =
=![]() =
=![]() ,
,
∴AQ+AP的最小值为![]() .
.