题目内容
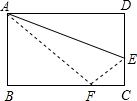 如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,求DE的长.
如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,求DE的长.
解:由折叠的性质知,DE=EF,AF=AD=12,
在Rt△ABF中,由勾股定理知,BF=4 ,FC=BC-BF=12-4
,FC=BC-BF=12-4 ,
,
在Rt△EFC中,由勾股定理知,FC2+CE2=EF2,
(8-EF)2+(12-4 )2=FE2,
)2=FE2,
解得EF=DE=(18-6 )cm.
)cm.
分析:在△ABF中,利用折叠及勾股定理易得BF长度,那么也就求得了CF的长度,用DE表示出EC,利用Rt△EFC是三边即可求得DE长度.
点评:此题主要考查了折叠的性质、矩形的性质,勾股定理等知识点.利用折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等得出是解题关键.
在Rt△ABF中,由勾股定理知,BF=4
 ,FC=BC-BF=12-4
,FC=BC-BF=12-4 ,
,在Rt△EFC中,由勾股定理知,FC2+CE2=EF2,
(8-EF)2+(12-4
 )2=FE2,
)2=FE2,解得EF=DE=(18-6
 )cm.
)cm.分析:在△ABF中,利用折叠及勾股定理易得BF长度,那么也就求得了CF的长度,用DE表示出EC,利用Rt△EFC是三边即可求得DE长度.
点评:此题主要考查了折叠的性质、矩形的性质,勾股定理等知识点.利用折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等得出是解题关键.

练习册系列答案
相关题目
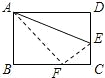 如图:把边长为AD=10cm,AB=8cm的矩形沿着AE为折痕对折,使点D落在BC上的点F处,则DE的长为( )
如图:把边长为AD=10cm,AB=8cm的矩形沿着AE为折痕对折,使点D落在BC上的点F处,则DE的长为( )| A、3cm | B、4cm | C、5cm | D、6cm |
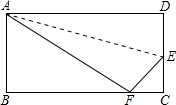 如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,则DE=
如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,则DE= 如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,求DE的长.
如图,把边长为AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,求DE的长.