题目内容
【题目】如图,ABCD中,E为AD边上一点,AE=AB,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,则tan∠GHB= 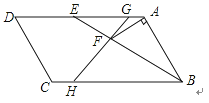
【答案】![]()
【解析】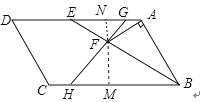
解;过F点作MN⊥BC,则MN⊥AD,设AG=a,
∵AG:GE=1:5,GE:BH=1:2,
∴EG=5a,BH=10a,AE=6a,
∵AE=AB,
∴AB=6a,∠AEB=∠ABE,
∵AD∥BC,
∴∠AEB=∠EBC,
∴BE是∠ABE的平分线,
∵FA⊥AB,FM⊥BC,
∴FM=FA,
在RT△ABF与RT△MBF中![]()
∴RT△ABF≌RT△MBF(HL),
∴BM=AB=6a,
∵∠AEB=∠EBC,∠EFG=∠BFH,
∴△EFG∽△BFH,![]() ,
,
∵FA=FM,
∴FN:FA=1:2,
在RT△AFN中,∠EAF=30°,
∵∠FAB=90°,
∴∠DAB=120°,
∴∠ABC=60°,
∴∠MBF=30°,
在RT△MBF中,FM=tan30°BM=![]() ×6a=2
×6a=2![]() a,
a,
∵BH=10a,BM=6a,
∴HM=BH﹣BM=4a,
∴tan∠GHB=![]() .
.
根据相似三角形对应高的比等于相似比,求得∠NAF=30°,进而求得∠DAB=120°,从而求得∠FBM=30°,根据正切定理求得FM,设GA=a,根据三角形相似求得BH=2EG=10a,根据三角形全等求得MB=AB=6a,从而求得HM=4a,在RT△FHM中根据正切定理即可求得

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目