题目内容
如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为 ▲ .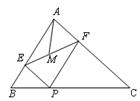

6
设BE=x,则AE=6-x,
∵在Rt△ABC中,AB=6,AC=8,
∴BC=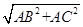 =10,
=10,
∴cos∠B="AB/BC" ="3/5" ,cos∠C="AC/AB" ="4/5" ,
∵PE⊥AB,PF⊥AC,
∴在Rt△BPE中,BP=BE/cos∠B =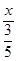 =
= 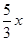 ,
,
∴CP="BC-BP=10-"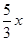 ,
,
在Rt△CPF中,CF=CP•cos∠C=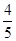 (10-
(10-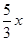 )="8-"
)="8-" 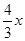 ,
,
∴AF=AC-CF=8-(8-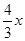 )=
)= 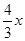 ,
,
∴S△AEF=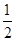 AE•AF=
AE•AF=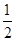 (6-x)•
(6-x)•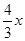 =-
=-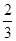 (x2-6x)=-
(x2-6x)=-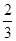 (x-3)2+6,
(x-3)2+6,
∴△AEF面积最大为6.
∵在Rt△ABC中,AB=6,AC=8,
∴BC=
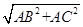 =10,
=10,∴cos∠B="AB/BC" ="3/5" ,cos∠C="AC/AB" ="4/5" ,
∵PE⊥AB,PF⊥AC,
∴在Rt△BPE中,BP=BE/cos∠B =
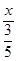 =
= 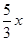 ,
,∴CP="BC-BP=10-"
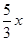 ,
,在Rt△CPF中,CF=CP•cos∠C=
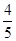 (10-
(10-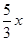 )="8-"
)="8-" 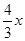 ,
,∴AF=AC-CF=8-(8-
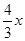 )=
)= 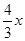 ,
,∴S△AEF=
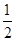 AE•AF=
AE•AF=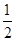 (6-x)•
(6-x)•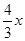 =-
=-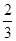 (x2-6x)=-
(x2-6x)=-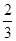 (x-3)2+6,
(x-3)2+6,∴△AEF面积最大为6.

练习册系列答案
相关题目
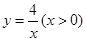 的图像上,点B在反比例函数
的图像上,点B在反比例函数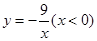 的图像上,且∠AOB=90°,则tan∠OAB的值为 ▲ .
的图像上,且∠AOB=90°,则tan∠OAB的值为 ▲ .
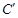 处,得折痕EF;
处,得折痕EF;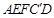 折叠,使AE、
折叠,使AE、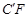 重合,得折痕DG,再打开;
重合,得折痕DG,再打开;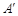 处,点E、F落在点
处,点E、F落在点 处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.
处,得折痕MN、QP.这样,就可以折出一个五边形DMNPQ.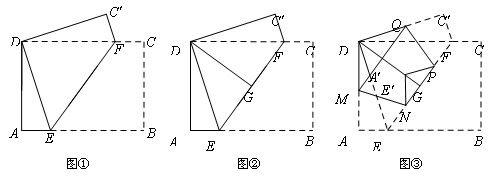
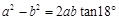 ; ②
; ②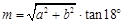 ;
;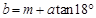 ; ④
; ④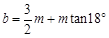 .
.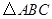 中,
中,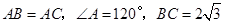 ,
,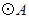 与
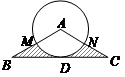
与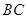 相切于点
相切于点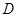 ,且交
,且交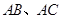 于
于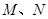 两点,则图中阴影部分的面积是 (保留
两点,则图中阴影部分的面积是 (保留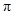 ).
).
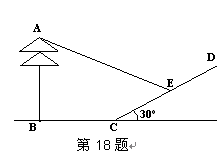
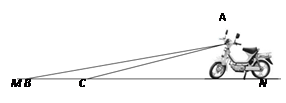
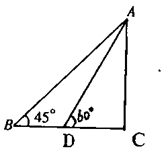
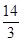 m,请判断该车大灯的设计是否能满足最小安全距离的要求,
m,请判断该车大灯的设计是否能满足最小安全距离的要求,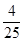 ,tan8°≈
,tan8°≈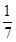 ,sin10°≈
,sin10°≈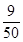 ,tan10°≈
,tan10°≈ )
)
 )
)
 +
+ -
-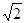 sin45º+(-2)0.
sin45º+(-2)0.