题目内容
【题目】如图,在平面直角坐标系中,顶点为(11,﹣![]() )的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,8).
)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,8).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)连接AC,在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形,若存在,请直接写出点P的坐标,若不存在,请说明理由.
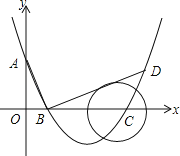
【答案】(1)![]() ;(2)对称轴l与⊙C相交,见解析;(3)P(30,﹣2)或(46,100)
;(2)对称轴l与⊙C相交,见解析;(3)P(30,﹣2)或(46,100)
【解析】
(1)已知抛物线的顶点坐标,可用顶点式设抛物线的解析式,然后将A点坐标代入其中,即可求出此二次函数的解析式;
(2)根据抛物线的解析式,易求得对称轴l的解析式及B、C的坐标,分别求出直线AB、BD、CE的解析式,再求出CE的长,与到抛物线的对称轴的距离相比较即可;
(3)分∠ACP=90°、∠CAP=90°两种情况,分别求解即可.
解:(1)设抛物线为y=a(x﹣11)2﹣![]() ,
,
∵抛物线经过点A(0,8),
∴8=a(0﹣11)2﹣![]() ,
,
解得a=![]() ,
,
∴抛物线为y=![]() =
=![]() ;
;
(2)设⊙C与BD相切于点E,连接CE,则∠BEC=∠AOB=90°.
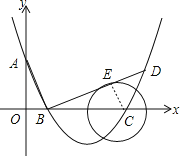
∵y=![]() =0时,x1=16,x2=6.
=0时,x1=16,x2=6.
∴A(0,8)、B(6,0)、C(16,0),
∴OA=8,OB=6,OC=16,BC=10;
∴AB=![]() =
=![]() =10,
=10,
∴AB=BC.
∵AB⊥BD,
∴∠ABC=∠EBC+90°=∠OAB+90°,
∴∠EBC=∠OAB,
∴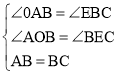 ,
,
∴△OAB≌△EBC(AAS),
∴OB=EC=6.
设抛物线对称轴交x轴于F.
∵x=11,
∴F(11,0),
∴CF=16﹣11=5<6,
∴对称轴l与⊙C相交;
(3)由点A、C的坐标得:直线AC的表达式为:y=﹣![]() x+8,
x+8,
①当∠ACP=90°时,
则直线CP的表达式为:y=2x﹣32,
联立直线和抛物线方程得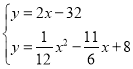 ,
,
解得:x=30或16(舍去),
故点P(30,﹣2);
当∠CAP=90°时,
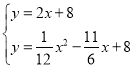
同理可得:点P(46,100),
综上,点P(30,﹣2)或(46,100);

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】10月下旬,我校初三年级组织了体育期中测试.为了更好的了解孩子们的体育水平,全力备战中考,我校体育组从全年级体考成绩中随机抽查了20名男生和20名女生的体考成绩进行整理、描述和分析(成绩得分用x表示,共分成四组:A:47<x≤50,B:44<x≤47,C:41<x≤44,D:x≤41),下面给出了部分信息:20名男生的体考成绩(单位:分):50,46,50,50,47,49,39,46,49,46,46,43,49,47,40,48,44,42,45,44;20名女生的体考成绩为B等级的数据是:45,46,46,47,47,46,46.所抽取的学生体考成绩统计表
性别 | 平均数 | 中位数 | 众数 |
男 | 46 | 46 | b |
女 | 46.5 | c | 48 |
根据以上信息,解答下列问题:
(1)直接写出上述图表中a、b、c的值;
(2)根据以上数据,你认为我校男生的体育成绩好还是女生的体育成绩好?请说明理由(一条即可);
(3)我校初三年级共有2400名学生参与此次体考测试,估计参加测试的学生等级为A的有多少人?