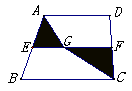题目内容
如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,点P、Q分别是边AD和AE上的动点(两动点都不与端点重合).
(1)PQ+DQ的最小值是 ;
(2)说出PQ+DQ取得最小值时,点P、点Q的位置,并在图8中画出;
(3)请对(2)中你所给的结论进行证明.

(1)PQ+DQ的最小值是 ;
(2)说出PQ+DQ取得最小值时,点P、点Q的位置,并在图8中画出;
(3)请对(2)中你所给的结论进行证明.

(1) 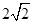 (2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析
(2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析
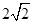 (2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析
(2)过点Q作QP⊥AD,垂足即为点P(3)证明见解析解:(1) 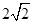 ;…………………………………………………………2分
;…………………………………………………………2分
(2)如图4,过点D作DF⊥AC,垂足为F,………………………3分
DF与AE的交点即为点Q;………………………………………………4分
过点Q作QP⊥AD,垂足即为点P;……………………………………5分
(3)由(2)知,DF为等腰Rt△ADC底边上的高,
∴DF=AD·sin45°=4×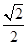 =
=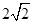 .…………………………6分
.…………………………6分
∵AE平分∠DAC,Q为AE上的点,
且QF⊥AC于点F,QP⊥AD于点P,
∴QP=QF(角平分线性质定理),……………………………………7分
∴PQ+DQ=FQ+DQ=DF=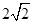 .
.
下面证明此时的PQ+DQ为最小值:
在AE上取异于Q的另一点Q1(图5).…………………………………9分
①过Q1点作Q1F1⊥AC于点F1,………………………………………10分
过Q1点作Q1P1⊥AD于点P1,…………………………………………11分
则P1Q1+DQ1=F1Q1+DQ1,
由“一点到一条直线的距离”,可知,垂线段最短,
∴得F1Q1+DQ1>FQ+DQ,
即P1Q1+DQ1>PQ+DQ.…………………………………………12分
②若P2是AD上异于P1的任一点,………………………………………13分
可知斜线段P2Q1>垂线段P1Q1,………………………………………14分
∴P2Q1+DQ1>P1Q1+DQ1>PQ+DQ.
从而可得此处PQ+DQ的值最小.
此题考核正方形的性质,利用垂线段最短求证最小值
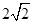 ;…………………………………………………………2分
;…………………………………………………………2分(2)如图4,过点D作DF⊥AC,垂足为F,………………………3分
DF与AE的交点即为点Q;………………………………………………4分
过点Q作QP⊥AD,垂足即为点P;……………………………………5分
(3)由(2)知,DF为等腰Rt△ADC底边上的高,
∴DF=AD·sin45°=4×
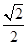 =
=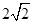 .…………………………6分
.…………………………6分∵AE平分∠DAC,Q为AE上的点,
且QF⊥AC于点F,QP⊥AD于点P,
∴QP=QF(角平分线性质定理),……………………………………7分
∴PQ+DQ=FQ+DQ=DF=
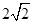 .
.下面证明此时的PQ+DQ为最小值:
在AE上取异于Q的另一点Q1(图5).…………………………………9分
①过Q1点作Q1F1⊥AC于点F1,………………………………………10分
过Q1点作Q1P1⊥AD于点P1,…………………………………………11分
则P1Q1+DQ1=F1Q1+DQ1,
由“一点到一条直线的距离”,可知,垂线段最短,
∴得F1Q1+DQ1>FQ+DQ,
即P1Q1+DQ1>PQ+DQ.…………………………………………12分
②若P2是AD上异于P1的任一点,………………………………………13分
可知斜线段P2Q1>垂线段P1Q1,………………………………………14分
∴P2Q1+DQ1>P1Q1+DQ1>PQ+DQ.
从而可得此处PQ+DQ的值最小.
此题考核正方形的性质,利用垂线段最短求证最小值

练习册系列答案
相关题目
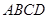 是矩形纸片,翻折∠
是矩形纸片,翻折∠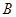 、∠
、∠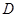 使
使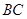 边、
边、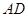 边恰好落在
边恰好落在 上。设
上。设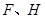 分别是
分别是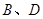 落在AC上的两点,
落在AC上的两点,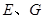 分别是折痕
分别是折痕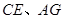 与
与 的交点。
的交点。
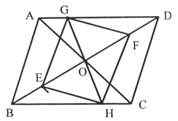

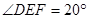 ,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的
,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的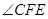 的度数是 (▲ )
的度数是 (▲ )
 的中位线
的中位线 上任意一点,若梯形
上任意一点,若梯形