题目内容
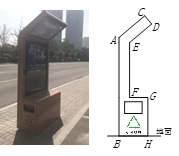
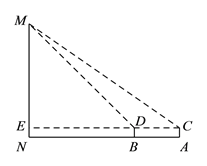
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

【答案】人民英雄纪念碑MN.的高度约为36.5米.
【解析】试题分析:由题意得,四边形ACDB,ACEN为矩形,从而得EN=AC=1.5.AB=CD=15,在Rt△MED中,由题意可得ME=DE,设ME=DE=x,则EC=x+15,在Rt△MEC中,可得ME=ECtan∠MCE,从而有x≈0.7(x+15),求出x的值,从而得MN=ME+EN≈36.5 .
试题解析:由题意得,四边形ACDB,ACEN为矩形,
∴EN=AC=1.5,AB=CD=15,
在![]() 中,
中,
∠MED=90°,∠MDE=45°,
∴∠EMD=∠MDE=45°,
∴ME=DE,
设ME=DE=x,则EC=x+15,
在![]() 中,∠MEC=90°,
中,∠MEC=90°,
∠MCE=35°,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴人民英雄纪念碑MN.的高度约为36.5米.

练习册系列答案
相关题目