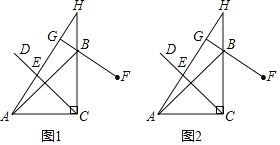
题目内容
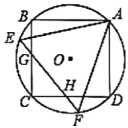
【题目】如图,正方形![]() 和正三角形
和正三角形![]() 都内接于
都内接于![]() ,
,![]() 与
与![]() ,
,![]() 分别相交于点
分别相交于点![]() ,
,![]() ,则
,则![]() 的值是________.
的值是________.
【答案】![]()
【解析】
设⊙O的半径是r,则OF=r,求出∠COF=60°,在Rt△OIF中,求出FI和OI的值,进而得到CI和EF的值,再根据EF∥BD,得出△CGH∽△CBD,根据相似三角形的性质求出GH的值即可.
解:如图,连接AC、BD、OF,AC与EF交于点I,
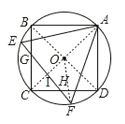
设⊙O的半径是r,则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∵AC⊥EF,
∴FI=r·sin60°=![]() ,OI=
,OI=![]()
∴EF=2FI=![]() ,CI=
,CI=![]() ,
,
∵AC⊥EF,AC⊥BD,
∴EF∥BD,
∴△CGH∽△CBD,
∴![]() ,
,
∴GH=![]() BD=r,
BD=r,
∴![]() .
.
故答案为:![]() .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
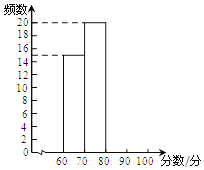
倍速训练法直通中考考点系列答案【题目】某学校组织七年级学生进行“垃圾分类”知识测试,现随机抽取部分学生的成绩进行统计,并绘制如下频数分布表以及频数分布直方图.
分数档 | 分数段/分 | 频数 | 频率 |
A | 90<x≤100 | a | 0.12 |
B | 80<x≤90 | b | 0.18 |
C | 70<x≤80 | 20 | c |
D | 60<x≤70 | 15 | d |
请根据以上信息,解答下列问题:
(1)已知A,B档的学生人数之和等于D档学生人数,求被抽取的学生人数,并把频数分布直方图补充完整.
(2)该校七年级共有200名学生参加测试,请估计七年级成绩在C档的学生人数.
(3)你能确定被抽取的这些学生的成绩的众数在哪一档吗?请说明理由.
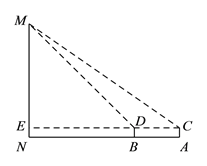
【题目】如图,⊙O的直径AB=4cm,点C为线段AB上一动点,过点C作AB的垂线交⊙O于点D,E,连结AD,AE.设AC的长为xcm,△ADE的面积为ycm2.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了y与x的几组对应值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
(3)如图,建立平面直角坐标系xOy,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
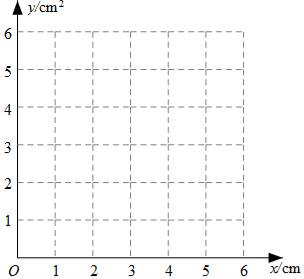
(4)结合画出的函数图象,解决问题:当△ADE的面积为4cm2时,AC的长度约为 cm.