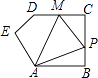��Ŀ����
����Ŀ���о�����ͼ�Σ����������ȸ�������ͼ�εĶ��壬���о��������ʺ��ж����������Ǹ������¶��壺��ͼ���ı���ABCD�У�AB=AD��CB=CD�����������ڱ߷ֱ���ȵ��ı��ν��������Ρ���
��1��С����Ϊ����������ġ����Ρ�������Ϊ�����ж���ȷ��
��2��С�ĸ���ѧϰ����ͼ�εľ��飬ͨ���۲졢ʵ�顢���ɡ���ȡ����롢֤���ȷ�������AB��BC�ġ����Ρ������ʺ��ж�����������̽����������С��̽���Ĺ��̣��벹����ɣ�
�������ȷ��������ࡰ���Ρ���һ��Խ���ȣ���������֤�����������С�ĵ�֤�����̣�
��֪����ͼ���ڡ����Ρ�ABCD�У�AB=AD��CB=CD��
��֤����ABC=��ADC��
֤������С���ɢٵõ������ࡰ���Ρ��ǵ����ʣ�����һ��̽���������ࡰ���Ρ��������������ʣ�����д�����ࡰ���Ρ���һ�����ʣ��������Ρ��Ķ����⣩��
�ۼ�����̽����С��̽�������ࡰ���Ρ����ж�������д�����ࡰ���Ρ���һ���ж��������������Ρ��Ķ����⣩��
���𰸡�
��1��
֤������ȷ��
�������ı���ȣ�
������������ġ����Ρ�
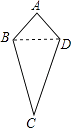
��2������BD���ڡ�ABD�͡�BCD�У�
��AB=AD��BC=CD��
���ABD=��ADB����DBC=��BDC
���ABC=��ADC�������Ρ���һ���Խ���ƽ��һ��Խǣ���һ���Խ��ߴ�ֱƽ����һ���Խ��ߵ��ı���������
��������֤������2��������BD���ڡ�ABD�͡�BCD�У�
��AB=AD��BC=CD��
���ABD=��ADB����DBC=��BDC
���ABC=��ADC��
�ڡ����Ρ���һ���Խ���ƽ��һ��Խǣ��𰸲�Ψһ����
����AC��BD��
��AB=AD��
��A��BD�Ĵ�ֱƽ�����ϣ�
��BC=DC��
��C��BD�Ĵ�ֱƽ�����ϣ�
��AC��BD�Ĵ�ֱƽ���ߣ�
��AB=AD��BC=CD��
��ACƽ�֡�BAC�͡�BCD��
�ࡰ���Ρ���һ���Խ���ƽ��һ��Խǣ�
���Դ��ǣ������Ρ���һ���Խ���ƽ��һ��Խǣ�
����һ���Խ��ߴ�ֱƽ����һ���Խ��ߵ��ı��������Σ��𰸲�Ψһ����
���Դ��ǣ���һ���Խ��ߴ�ֱƽ����һ���Խ��ߵ��ı��������Σ�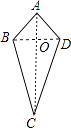

 ��У����ϵ�д�
��У����ϵ�д�