题目内容
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
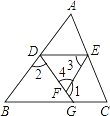
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=________.(________.),
∴AB∥EF(________.)
∴∠3=________.(________.)
又∠B=∠3(已知)
∴∠B=________.(等量代换)
∴DE∥BC(________.)
∴∠C=∠AED(________.).
【答案】 ∠DFE; 同角的补角相等; 内错角相等,两直线平行; ∠ADE; 两直线平行,内错角相等; ∠ADE; 同位角相等,两直线平行; 两直线平行,同位角相等
【解析】根据平行线的判定及性质即可证明.
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=∠DFE.(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE.(两直线平行,内错角相等)
又∠B=∠3(已知)
∴∠B=∠ADE.(等量代换)
∴DE∥BC(同位角相等,两直线平行)
∴∠C=∠AED(两直线平行,同位角相等).

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
