题目内容
【题目】如图，正方形ABCD中，AB=2，动点P从点B出发，以每秒1个单位的速度在正方形的边上沿BC-CD-DA运动，设运动时间为t,△PAB面积为S.
(1)求S关于t的函数解析式，并写出自变量t的取值范围;
(2)画出相应函数图象;
(3)当S=
时，t的值为多少.
【答案】（1）S＝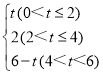
；（2）见解析；（3）1.5s或4.5s.
【解析】
（1）分三种情形画出图形，利用三角形的面积公式分别求解即可；
（2）画出分段函数的图象，注意自变量的取值范围；
（3）利用图象法解决问题即可．
解：（1）如图1中，当0＜t≤2时，S＝
BPAB＝×t×2＝t．
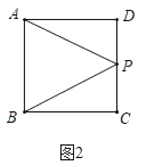
如图2中，当2＜t≤4时，S＝S正方形ABCD＝×2×2＝2．
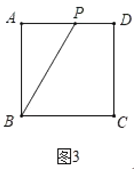
如图3中，当4＜t＜6时，S＝APAB＝×（6t）×2＝6t．
综上所述，S＝；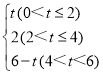
（2）函数图象如图所示：
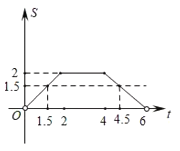
（3）当S＝
时，观察函数图象可知，t的值为1.5s或4.5s．
故答案为1.5s或4.5s．
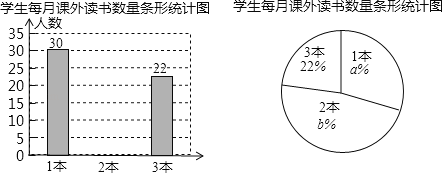
【题目】近年来，我国很多地区持续出现雾霾天气．某社区为了调查本社区居民对雾霾天气主要成因的认识情况，随机对该社区部分居民进行了问卷调查，要求居民从五个主要成因中只选择其中的一项，被调查居民都按要求填写了问卷．社区对调查结果进行了整理，绘制了如下不完整的统计图表．被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数（人数） |
A大气气压低，空气不流动 | m |
B地面灰尘大，空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题：
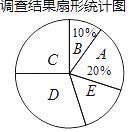
（1）填空：m=________，n=________，扇形统计图中C选项所占的百分比为________．
（2）若该社区居民约有6 000人，请估计其中会选择D选项的居民人数．
（3）对于“雾霾”这个环境问题，请你用简短的语言发出倡议．
