题目内容
【题目】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是 . 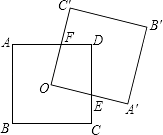
【答案】1
【解析】解:如图,连接AC,BD,正方形ABCD的对角线相交于点O,∴∠ODE=∠OAF=45°,OA=OD,∠AOD=90°,
∵∠EOF=∠DOE+∠DOF=90°,∠AOD=∠DOF+∠AOF=90°,
∴∠DOE=∠AOF,
在△DOE和△AOF中,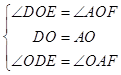 ,
,
∴△DOE≌△AOF(ASA),
∴S△AOF=S△DOE ,
∴四边形OEDF的面积=S△DOE+S△DOF=S△AOF+S△DOF=S△AOD ,
∵S△AOD= ![]() S正方形ABCD=
S正方形ABCD= ![]() ×2×2=1,
×2×2=1,
∴四边形OEDF的面积为1,即两个正方形重叠部分的面积为1.
故答案为:1.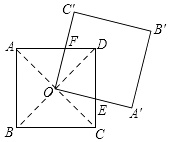
根据正方形性质可得∠ODE=∠OAF=45°,OA=OD,∠AOD=90°,即可求得∠DOE=∠AOF,即可判定△DOE≌△AOF,可得S△AOF=S△DOE , 即可求得两个正方形重叠部分的面积=S△AOD .

【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:

(1)根据上面多面体的模型,完成表格中的空格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 12 | |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是E=________;
(3)一个多面体的面数比顶点数大8,棱数为30,则这个多面体的面数是多少?
【题目】某茶叶厂用甲,乙,丙三台包装机分装质量为200g的茶叶,从它们各自分装的茶叶中分别随机抽取了20盒,得到它们的实际质量的方差如下表所示:
甲包装机 | 乙包装机 | 丙包装机 | |
方差 | 10.96 | 5.96 | 12.32 |
根据表中数据,可以认为三台包装机中,包装茶叶的质量最稳定是_____.