Question

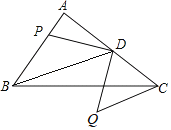
【题目】如图，在Rt△ABC中，∠A＝90°，AB＝4，AC＝6，点D为AC中点，点P为AB上的动点，将点P绕点D逆时针旋转90°得到点Q，连接CQ，则线段CQ的最小值为_____．

Answer 1

【答案】3

【解析】

过Q作QE⊥AC于E，易证△DAP≌△QED，可得QE＝AD＝3，再根据当AP＝DE＝3时，DE＝DC，即点E与点C重合，即可得出线段CQ的最小值为3．

如图所示，过Q作QE⊥AC于E，则∠A＝∠QED＝90°，

由旋转可得，DP＝QD，∠PDQ＝90°，

∴∠ADP＝∠EQD，

在△DAP和△QED中，

，

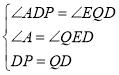∴△DAP≌△QED（AAS），

∴QE＝AD＝AC＝3，

∴当AP=DE=3时，DE=DC，即点E与点C重合，

此时CQ=EQ=3，

∴当点E与点C重合，CQ的值最小，CQ的最小值为3，

故答案为：3．